题目内容
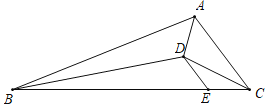
【题目】如图1，分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC，EG剪开，拼成如图2所示的ALMN，若中间空白部分四边形OPQR恰好是正方形，且ALMN的面积为50，则正方形EFGH的面积为（ ）
A. 24 B. 25 C. 26 D. 27
【答案】B
【解析】
此题涉及的知识点是正方形、长方形的性质，先根据正方形和长方形的性质求出各边长的关系，再根据ALMN的面积，求出各边长的关系，最后得出面积.
设EF=a，BC=b，AB=c，则PQ=a-c，RQ=b-a，PQ=RQ
∴a=
，
∵ALMN的面积为50，∴bc+a2+(a-c)2=50,
把a=代入化简求值得b+c=10, ∴a=5,
∴正方形EFGH的边长为5，
∴正方形EFGH的面积为25，
故选B.
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
【题目】国家教育部提出“每天锻炼一小时，健康工作五十年，幸福生活一辈子”.万州区某中学对九年级部分学生进行问卷调查“你最喜欢的锻炼项目是什么？”，规定从“打球”，“跑步”，“游泳”，“跳绳”，“其他”五个选项中选择自己最喜欢的项目，且只能选择一个项目，并将调查结果绘制成如下两幅不完整的统计图.
最喜欢的锻炼项目 | 人数 |
打球 | 120 |
跑步 |
|
游泳 |
|
跳绳 | 30 |
其他 |
|
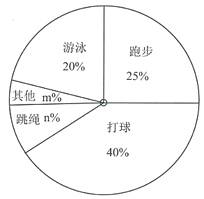
（1）这次问卷调查的学生总人数为 ，人数
；
（2）扇形统计图中，
，“其他”对应的扇形的圆心角的度数为 度；
（3）若该年级有1200名学生，估计喜欢“跳绳”项目的学生大约有多少人？
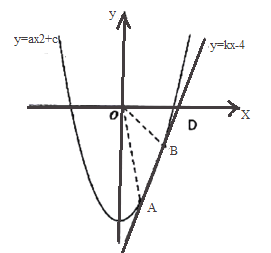
【题目】有这样一个问题：探究函数y＝(x﹣1)(x﹣2)(x﹣3)的图象与性质.小东对函数y＝(x﹣1)(x﹣2)(x﹣3)的图象与性质进行了探究.下面是小东的探究过程，请补充完成：
(1)函数y＝(x﹣1)(x﹣2)(x﹣3)的自变量x的取值范围是_______；
(2)下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | m | ﹣24 | ﹣6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
①m＝_____；
②若M(﹣7，﹣720)，N(n，720)为该函数图象上的两点，则n＝_____；
(3)在平面直角坐标系xOy中，A(xA，yA)，B(xB，﹣yA)为该函数图象上的两点，且A为2≤x≤3范围内的最低点，A点的位置如图所示.
①标出点B的位置；
②画出函数y＝(x﹣1)(x﹣2)(x﹣3)(0≤x≤4)的图象.
③写出直线y＝
x﹣1与②中你画出图象的交点的横坐标之和为______.
