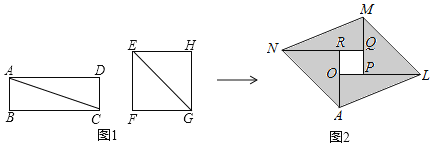题目内容
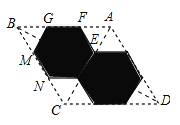
【题目】校园内有一个由两个全等的六边形(边长为![]() )围成的花坛,现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为( )
)围成的花坛,现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根据题意和正六边形的性质得出△BMG是等边三角形,再根据正六边形的边长得出BG=GM=3.5m,同理可证出AF=EF=3.5m,再根据AB=BG+GF+AF,求出AB,从而得出扩建后菱形区域的周长.
解:如图,∵花坛是由两个相同的正六边形围成,
∴∠FGM=∠GMN=120°,GM=GF=EF,
∴∠BMG=∠BGM=60°,
∴△BMG是等边三角形,
∴BG=GM=3.5(m),
同理可证:AF=EF=3.5(m)
∴AB=BG+GF+AF=3.5×3=10.5(m),
∴扩建后菱形区域的周长为10.5×4=42(m),
故选:C.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目