Question

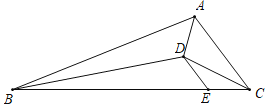
【题目】在△ABC中，AC＝6，AB＝14，BC＝16，点D是△ABC的内心，过D作DE∥AC交BC于E，则DE的长为（　　）

A.B.C.D.

Answer 1

【答案】C

【解析】

过点B作BH∥AC，交AD的延长线于点H，由内心的性质可证AB＝BH＝14，DE＝EC，通过证明△ACF∽△HBF，可求CF的长，通过证明△DEF∽△ACF，可求DE的长．

解：如图，过点B作BH∥AC，交AD的延长线于点H，

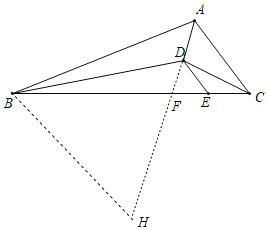
∵点D是△ABC的内心，

∴∠BAD＝∠CAD，∠ACD＝∠DCB，

∵DE∥AC，BH∥AC，

∴∠H＝∠DAC，∠EDC＝∠ACD，

∴∠H＝∠BAD，∠EDC＝∠ECD，

∴AB＝BH＝14，DE＝EC，

∵BH∥AC，

∴△ACF∽△HBF，

∴，

∴

∴CF＝，

∵DE∥AC，

∴△DEF∽△ACF，

∴，

∴

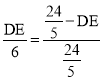
∴DE＝，

故选：C．