题目内容
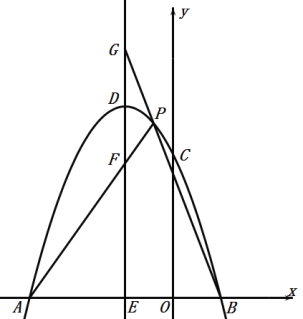
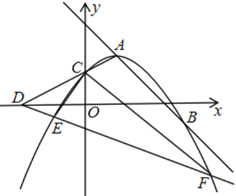
【题目】如图,抛物线y=![]() x2+mx+m(m>0)的顶点为A,交y轴于点C.
x2+mx+m(m>0)的顶点为A,交y轴于点C.
(1)求出点A的坐标(用含m的式子表示);
(2)若直线y=﹣x+n经过点A,与抛物线交于另一点B,证明:AB的长是定值;
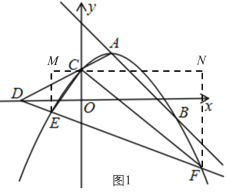
(3)连接AC,延长AC交x轴于点D,作直线AD关于x轴对称的直线,与抛物线分别交于E、F两点.若∠ECF=90°,求m的值.
【答案】(1)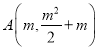 ;(2)见解析;(3)-1+
;(2)见解析;(3)-1+![]()
【解析】
(1)直接写出顶点式即可得出结论;
(2)先将点A坐标代入直线AB的解析式中,得出n=2m+![]() m2,进而得出直线AB的解析式为y=-x+2m+
m2,进而得出直线AB的解析式为y=-x+2m+![]() m2,再联立抛物线解析式得出方程组,转化成方程,利用根与系数的关系即可得出结论;
m2,再联立抛物线解析式得出方程组,转化成方程,利用根与系数的关系即可得出结论;
(3)先求出点A,C关于x轴的对称点,进而得出直线EF解析式,再联立抛物线解析式,过点C作MN∥x轴,过点E作EM⊥MN于点M,过点F作FN⊥MN,设点E,F坐标,联系抛物线和EF表达式,利用根与系数的关系列出方程求解.
解:(1)![]() 抛物线
抛物线![]() ,
,
![]() 顶点
顶点![]() 的坐标为
的坐标为![]() ;
;
(2)由(1)知,顶点![]() 的坐标为
的坐标为![]() ,
,
![]() 直线
直线![]() 经过点
经过点![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ①,
①,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 抛物线
抛物线![]() ②,
②,
联立①②得,![]() ,
,
即:![]() ,
,
![]() ,
,![]() ,
,
![]()
即:![]() 的长是定值,其值为
的长是定值,其值为![]() ;
;
(3)![]() 抛物线
抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,
![]() ,
,
![]() 点
点![]() 关于
关于![]() 轴的对称点的坐标为
轴的对称点的坐标为![]() ,
,
由(1)知,顶点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 关于
关于![]() 轴的对称点的坐标为
轴的对称点的坐标为![]() ,
,
![]() 直线
直线![]() 是直线
是直线![]() 关于
关于![]() 轴的对称点,
轴的对称点,
![]() 点
点![]() ,
,![]() 在直线
在直线![]() 上,
上,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ③,
③,
![]() 抛物线
抛物线![]() ④,
④,
设E(![]() ,
,![]() ),F(
),F(![]() ,
,![]() ),
),
过点C作MN∥x轴,过点E作EM⊥MN于点M,过点F作FN⊥MN,如图1,
∵∠ECF=90°,
∴∠ECM+∠FCN=90°,
∠FCN+∠CFN=90°,
∴∠ECM=∠CFN,
∵∠EMC=∠FNC=90°,
∴△EMC∽△CNF,
∴![]() ,
,
即![]() ,
,
化简得:![]() ,
,
联立③④得,![]() ,
,
![]() ,
,![]() ,
,
![]() =
=![]()
![]() =
=![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() =0
=0
解得:m=![]() 或m=
或m=![]() 或m=0,
或m=0,
∵m>0
∴m=![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案