Question

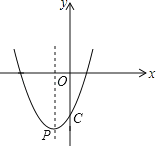
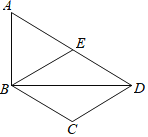
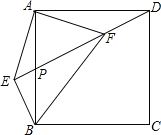
【题目】如图，在正方形ABCD中，点P是AB的中点，连接DP，过点B作BE⊥DP交DP的延长线于点E，连接AE，过A点作AF⊥AE交DP于点F，连接BF，若AE=2，正方形ABCD的面积为___．

Answer 1

【答案】10

【解析】

如图，由正方形性质和已知就可以得出∠EAF=∠DAB=90°，AB=AD，可以得出∠1=∠2，由对顶角相等可以得出∠5=∠6，所以∠3=∠4，从而可以证明△AEB≌△AFD，可以求得AE=AF，再利用勾股定理就可以求出EF的值，过点A作AM⊥EF于M，由△AEF是等腰直角三角形，可以得出∠AME=90°，由已知可以证明△AMP≌△BEP，可以得出BE=AM=，最后由勾股定理求出结论．

解：∵四边形ABCD是正方形，且BE⊥DP，AF⊥AE，
∴AB=AD，∠BAD=∠EAF=∠BEF=90°，
∴∠1+∠FAB=∠2+∠FAB=90°，
∴∠1=∠2．

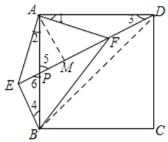
∵∠3+∠5=∠4+∠6，且∠5=∠6，
∴∠3=∠4．
在△AEB和△AFD中，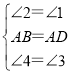
，
∴△AEB≌△AFD（ASA），
∴AE=AF=2，BE=DF，
∴△EAF为等腰直角三角形．
在Rt△EAF中，由勾股定理，得
EF==2．
过点A作AM⊥EF于M，连接BD，
∴AM=MF=EM=EF=，∠AME=∠BEF=90°，
∵点P是AB的中点，
∴AP=BP，
在△AMP和△BEP中，
，
∴△AMP≌△BEP（AAS），
∴BE=AM=DF=，
∴DE=EF+DF=2+=3，
在Rt△BED中，BD== ==2，
∴S正方形ABCD=BD2=×(2)2=10．
故答案为：10．