ΧβΡΩΡΎ»ί
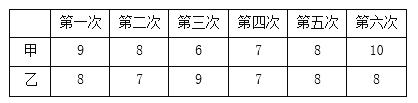
ΓΨΧβΡΩΓΩΡ≥…ΧΒξœζ έΟφœρ÷–ΩΦ…ζΒΡΦΤ ΐΧχ…ΰΘ§ΟΩΗυ≥…±ΨΈΣ20‘ΣΘ§œζ έΒΡ«Α40ΧλΡΎΒΡ»’œζ έΝΩmΘ®ΗυΘ©”κ ±ΦδtΘ®ΧλΘ©ΒΡΙΊœΒ»γ±μΘ°
±ΦδtΘ®ΧλΘ© | 1 | 3 | 8 | 10 | 26 | Γ≠ |
»’œζ έΝΩmΘ®ΦΰΘ© | 51 | 49 | 44 | 42 | 26 | Γ≠ |
«Α40ΧλΟΩΧλΒΡΦέΗώyΘ®‘Σ/ΦΰΘ©”κ ±ΦδtΘ®ΧλΘ©ΒΡΚ· ΐΙΊœΒ ΫΈΣΘΚy=![]() t+25Θ®1ΓήtΓή40«“tΈΣ’ϊ ΐΘ©ΘΜ
t+25Θ®1ΓήtΓή40«“tΈΣ’ϊ ΐΘ©ΘΜ
Θ®1Θ©»œ’φΖ÷Έω±μ÷–ΒΡ ΐΨίΘ§”ΟΥυ―ßΙΐΒΡ÷Σ Ε»ΖΕ®mΘ®ΦΰΘ©”κtΘ®ΧλΘ©÷°Φδ «¬ζΉψ“Μ¥ΈΚ· ΐΒΡΙΊœΒΜΙ «Εΰ¥ΈΚ· ΐΒΡΙΊœΒΘΩ≤Δάϊ”Ο’β–© ΐΨί«σmΘ®ΦΰΘ©”κtΘ®ΧλΘ©÷°ΦδΒΟΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©«κΦΤΥψ40Χλ÷–ΡΡ“ΜΧλΒΡ»’œζ έάϊ»σΉν¥σΘ§Ήν¥σ»’œζ έάϊ»σ «Εύ…ΌΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©m”κt¬ζΉψ“Μ¥ΈΚ· ΐΙΊœΒΘ§mΘΫ©¹t+52ΘΜΘ®2Θ©ΒΎ16Χλ ±Θ§œζ έάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ324‘ΣΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©¥”±μΗώΩ…Ω¥≥ωΟΩΧλ±»«Α“ΜΧλ…Όœζ έ1ΦΰΘ§Υυ“‘≈–ΕœΈΣ“Μ¥ΈΚ· ΐΙΊœΒ ΫΘ§¥ΐΕ®œΒ ΐΖ®«σΫβΩ…ΒΟΫβΈω ΫΘΜ
Θ®2Θ©»’άϊ»σ=»’œζ έΝΩΓΝΟΩΦΰάϊ»σΘ§Ψί¥Υ±μ ΨΟΩΧλΒΡ»’άϊ»σΘ§ΗυΨίΚ· ΐ–‘÷ «σΉν¥σ÷ΒΦ¥Ω…Θ°
Θ®1Θ©”…±μΗώ÷– ΐΨίΩ…÷ΣΘ§Β± ±ΦδtΟΩ‘ωΦ”1ΧλΘ§»’œζ έΝΩœύ”ΠΦθ…Ό1ΦΰΘ§Γύm”κt¬ζΉψ“Μ¥ΈΚ· ΐΙΊœΒΘ§…ηm=kt+bΘ§ΫΪΘ®1Θ§51Θ©ΓΔΘ®3Θ§49Θ©¥ζ»κΘ§ΒΟΘΚ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§Γύm”κtΒΡΚ· ΐΙΊœΒΈΣΘΚm=©¹t+52ΘΜ
Θ§Γύm”κtΒΡΚ· ΐΙΊœΒΈΣΘΚm=©¹t+52ΘΜ
Θ®2Θ©…η»’œζ έάϊ»σΈΣPΘ§‘ρ P=Θ®©¹t+52Θ©Θ®![]() t+25©¹20Θ©
t+25©¹20Θ©![]() Θ®t©¹16Θ©2+324Θ§ΓύΒ±t=16 ±Θ§P”–Ήν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ324‘ΣΘ°
Θ®t©¹16Θ©2+324Θ§ΓύΒ±t=16 ±Θ§P”–Ήν¥σ÷ΒΘ§Ήν¥σ÷ΒΈΣ324‘ΣΘ°
¥πΘΚΒΎ16Χλ ±Θ§œζ έάϊ»σΉν¥σΘ§Ήν¥σάϊ»σΈΣ324‘ΣΘ°