Question

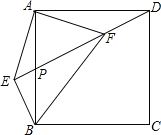
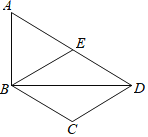
【题目】如图，在Rt△ABD中，∠ABD=90°，E为AD的中点，AD∥BC，BE∥CD．

（1）求证：四边形BCDE是菱形；

（2）连接AC，若AC平分∠BAD，BC=1，求AC的长．

Answer 1

【答案】（1）见解析；（2）AC=．

【解析】

（1）由AD∥BC，BE∥CD，推出四边形BCDE是平行四边形，再证明BE=DE即可解决问题；
（2）在Rt△ACD中只要证明∠ADC=60°，AD=2即可解决问题．

（1）证明：∵AD∥BC，BE∥CD，

∴四边形BCDE是平行四边形，

∵∠ABD=90°，E为AD的中点，

∴BE=DE= AD，

∴四边形BCDE是菱形．

（2）解：连接AC．

∵AD∥BC，AC平分∠BAD，

∴∠BAC=∠DAC=∠BCA，

∴AB=BC=1，

∵AD=2BC=2，

∴sin∠ADB= ，

∴∠ADB=30°，

∴∠DAC=30°，∠ADC=60°，

∴∠ACD=90°，

在Rt△ACD中，∵AD=2，

∴CD=1，AC=．