题目内容
【题目】如图,已知二次函数![]() 的顶点P的横坐标为
的顶点P的横坐标为![]() ,且与y轴交于点C(0,-4).
,且与y轴交于点C(0,-4).
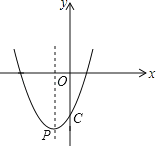
(1)求b,c的值;
(2)直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧)点M关于y轴的对称点为点M,点H的坐标为(3,0).若四边形ONMH的面积为18.求点H到OM的距离;
(3)是否在对称轴的同侧存在实数m、n(m<n),当![]() 时,y的取值范围为
时,y的取值范围为![]() ?若存在,求出m,n的值;若不存在,说明理由.
?若存在,求出m,n的值;若不存在,说明理由.
【答案】(1)b=3,c=-4;(2)![]() ;(3)
;(3)![]() 的取值范围为
的取值范围为![]() ,此时m=-3,n=-2
,此时m=-3,n=-2
【解析】
(1)根据二次函数顶点坐标公式和C点的坐标列出二元一次方程组,求出b、c的值.
(2)首先设设M(t,m),则N(3+t,m),M'(t,m),其中t>0,进而表示出M'N=3=OH,可知四边形ONM'H为平行四边形,从而求出四边形ONM'H的高.所以M(5,6),M'(5,6),N(2,6),再求出OM'的长度.最后根据三角形面积公式求出点H到OM′的距离;
(3)根据题意,分两种情况:①当![]() 时;②当
时;②当![]() 时;然后根据二次函数的最值的求法,求出满足题意的实数m、n(m<n),使得当m≤x≤n时,y的取值范围为为
时;然后根据二次函数的最值的求法,求出满足题意的实数m、n(m<n),使得当m≤x≤n时,y的取值范围为为![]() 即可.
即可.
解:(1)由题意可得,
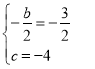 ,解得
,解得![]() ,
,![]() ;
;
(2)连接![]() .设
.设![]() ,则
,则![]() ,
,![]() ,其中
,其中![]() ,
,
![]() ,
,![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,![]() ,
,![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,![]() ,
,
![]() ,代入
,代入![]() ,得
,得![]() ,
,
解得![]() ,
,![]() (不符合题意,舍去),
(不符合题意,舍去),
![]() ,
,![]() ,
,![]()
![]()
又![]() ,
,
![]() 点
点![]() 到
到![]() 的距离
的距离![]() ;
;
(3)分两种情况讨论:
①当![]() ,即
,即![]() 、
、![]() 在对称轴的左侧时,二次函数
在对称轴的左侧时,二次函数![]() 的值随
的值随![]() 增大而减小,
增大而减小,
![]()
![]() ,
,
![]()
 ,(1)
,(1)![]() 得,
得,![]()
![]() ,解得
,解得![]() 或2或
或2或![]() ,同理由(2)得
,同理由(2)得
![]() 或2或3,
或2或3,
![]() ,
,![]() ,
,![]() ;
;
②当![]() ,即
,即![]() 、
、![]() 在对称轴的右侧时,二次函数
在对称轴的右侧时,二次函数![]() 的值随
的值随![]() 增大而增大,
增大而增大,
![]()
![]() ,
,
 ,(1)
,(1)![]() ,得
,得![]() ,
,

![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
将![]() 代入(2)
代入(2)
![]() ,
,![]()
![]() ,得
,得![]()
![]() ,与上述
,与上述![]() 矛盾,
矛盾,
![]() 没有满足的
没有满足的![]() 、
、![]() .
.
综上,在对称轴的左侧存在实数![]() 、
、![]() ,当
,当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,此时m=-3,n=-2.
,此时m=-3,n=-2.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案