题目内容
【题目】在Rt![]() 中,AB=BC=4,
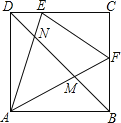
中,AB=BC=4,![]() ,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形.
,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形.
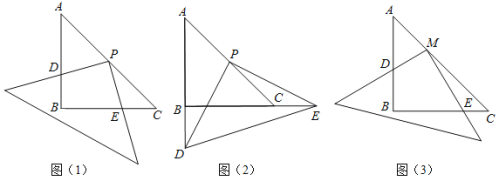
(1)直角三角板绕点P旋转过程中,当![]() ______时,
______时,![]() 是等腰三角形;
是等腰三角形;
(2)直角三角板绕点P旋转到图(1)的情形时,求证:PD=PE;
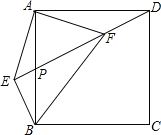
(3)如图(3),若将直角三角板的顶点放在斜边AC的点M处,设![]() (
(![]() 、
、![]() 为正数),求证:
为正数),求证:![]() .
.
【答案】(1)0,2,![]() 或
或![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)根据△PEC是等腰三角形,分类进行讨论即可;
(2)连接BP,首先根据题干条件证明出∠BPD=∠CPE,然后证明△DPB≌△EPC,于是证明出PD=PE;
(3)过M分别作AB、BC的垂线,垂足分别为G、H,首先根据角之间的关系求出∠GMD=∠HME,进而证明出△MGD∽△MHE,根据相似三角形对应边成比例,得到![]() ,再求出GM、HM关于m、n的表达式,三式结合求出MD、ME之间的比例关系.
,再求出GM、HM关于m、n的表达式,三式结合求出MD、ME之间的比例关系.
解:(1)当BE=0时,即点B和点E重合,故可知△PEC是等腰三角形,
当BE=2时,即E是BC的中点,可得△PEC是等腰三角形
由题干条件知PC=![]() ,当CP=CE时△PEC是等腰三角形,BE=4
,当CP=CE时△PEC是等腰三角形,BE=4![]() ;
;
当E在BC的延长线上时,CE=CP,△PEC是等腰三角形,BE=4+![]() ;
;
故答案为:0或2或4![]() 或4+
或4+![]() ;
;
(2)连接BP.
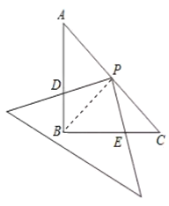
∵AB=BC 且∠ABC=90°,
∴∠C=45°,
又∵P是AC中点,
∴BP⊥AC,BP=PC 且∠ABP=∠CBP=45°,
∴∠CPE+∠EPB=90°,
∵DP⊥PE,
∴∠BPD+∠EPB=90°,
∴∠BPD=∠CPE,
在△DPB和△EPC中,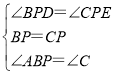 ,
,
∴△DPB≌△EPC,
∴PD=PE;
(3)过M分别作AB、BC的垂线,垂足分别为G、H.
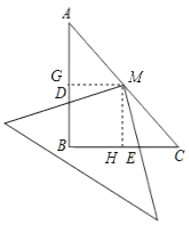
由作图知,∠MGA=∠MGB=∠MHB=∠MHE=90°
又∵∠B=90°,
∴∠GMH=90°,
∴∠GMD+∠DMH=90°,
∵∠DMH+∠HME=90°,
∴∠GMD=∠HME
∴△MGD∽△MHE,
∴![]() ①,
①,
∵![]() ,
,
∴![]() ,
,
∵∠MGA=∠B=90°,
∴GM∥BC,
∴![]() ,即GM=BC
,即GM=BC![]() ②
②
同理 HM=AB![]() ,
,
∵AB=BC,
∴HM=BC![]() ③
③
②③代入①得:![]() .
.

 阅读快车系列答案
阅读快车系列答案