题目内容
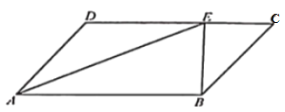
【题目】如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求证:∠BEC=90°;
(2)求cos∠DAE.
【答案】(1)见解析;(2)cos∠DAE=![]()
【解析】
(1)先求出BC的长,继而根据勾股定理的逆定理进行证明即可得;
(2)根据平行四边形的性质可求得AB=16,∠ABE=90°,继而根据勾股定理求出AE的长,然后利用余弦的定义求出cos∠EAB的值,再根据∠DAE=∠EAB即可求得答案.
(1)∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC ,
∴∠AED=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠AED=∠DAE,
∴AD=DE=10,
∴BC=10,
又∵BE=8,CE=6,
∴BE2+CE2=BC2,
∴△BEC为直角三角形,
∴∠BEC=90°;
(2)∵ DE=10,CE=6,
∴CD=DE+CE=16,
∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD=16,
∴∠ABE=∠BEC=90°,
∴AE=![]() ,
,
∴cos∠EAB=![]() ,
,
∵∠DAE=∠EAB,
∴cos∠DAE==![]() .
.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目