题目内容
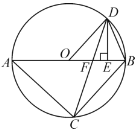
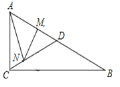
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,点
,点![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 不与
不与![]() 两点重合),连接
两点重合),连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() .
.
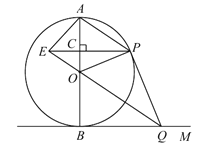
(1)求证:![]() .
.
(2)若直径![]() 的长为12.
的长为12.
①当![]() ________时,四边形
________时,四边形![]() 为正方形;
为正方形;
②当![]() ________时,四边形
________时,四边形![]() 为菱形.
为菱形.
【答案】(1)见解析;(2)①6;②![]()
【解析】
(1)根据切线的性质得![]() ,再根据平行线的性质得
,再根据平行线的性质得![]() ,
,![]() ,加上
,加上![]() ,则
,则![]() ,即可证明
,即可证明![]() .
.
(2)①利用![]() 得到
得到![]() ,由于
,由于![]() ,所以当
,所以当![]() ,四边形OPQB为正方形,此时点C、点E与点O重合,于是
,四边形OPQB为正方形,此时点C、点E与点O重合,于是![]() .②根据菱形的判定,当
.②根据菱形的判定,当![]() ,四边形AEOP为菱形,则
,四边形AEOP为菱形,则![]() ,然后利用勾股定理计算出PC,从而得到PE的长.
,然后利用勾股定理计算出PC,从而得到PE的长.
(1)证明:∵![]() 切
切![]() 于点
于点![]()
∴![]()
∵![]()
∴![]() ,
,![]()
又∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
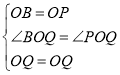
∴![]()
(2)①正方形![]()
![]()
![]()
∴当![]() 时,四边形OPQB为矩形,而
时,四边形OPQB为矩形,而![]() ,则四边形OPQB为正方形,而此时
,则四边形OPQB为正方形,而此时![]() 三点重合
三点重合
∴![]()
②菱形![]()
![]()
∴当![]() ,
,![]() ,四边形AEOP为菱形
,四边形AEOP为菱形
∵![]()
∴![]()
![]()
∴![]()

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目