题目内容
【题目】如图，在锐角△ABC中，AB=5
，∠BAC=45°，∠BAC的平分线交BC于点D，M，N分别是AD，AB上的动点，则BM+MN的最小值是______．
【答案】5
【解析】
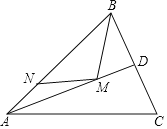
作BH⊥AC，垂足为H，交AD于M点，过M点作MN⊥AB，垂足为N，则BM+MN为所求的最小值，再根据AD是∠BAC的平分线可知MH=MN，再由等腰直角三角形的性质即可得出结论．
如图，作BH⊥AC，垂足为H，交AD于M点，过M点作MN⊥AB，垂足为N，则BM+MN为所求的最小值．
∵AD是∠BAC的平分线，∴MH=MN，∴BH是点B到直线AC的最短距离（垂线段最短）．
∵AB=5
，∠BAC=45°，∴BH=
=
5．
∵BM+MN的最小值是BM+MN=BM+MH=BH=5．
故答案为5．
练习册系列答案
阅读快车系列答案
相关题目
