Question

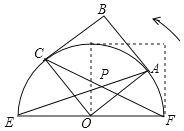
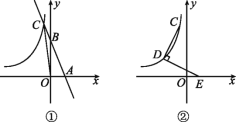
【题目】如图①，直线y=-2x+4交x轴、y轴于A，B两点，交双曲线y=(x<0)于C点，△OAC的面积为6．

(1)求双曲线的解析式；

(2)如图②，D为双曲线y=(x<0)上一点，连接CD，将线段CD绕点D顺时针旋转90°得线段DE，点E恰好落在x轴上，求点E的坐标．

Answer 1

【答案】（1）y=-；（2）点E的坐标为(1，0)

【解析】

（1）过C作CH⊥x轴于H，根据△AOC的面积为6，求得CH=6，即可得出C（-1，6），代入y=（x＜0）可得，k=-6；
（2）过点D作DF⊥x轴于F，过C作CG⊥DF于G，则∠G=∠DFE=90°，再根据旋转的性质，判定△DCG≌△EDF（AAS），即可得出CG=DF，DG=EF，再设D（m，-），则DF=-，FO=-a，根据C（-1，6），可得CG=-1-m，DF=-1-m，进而得出方程-=-1-m，解得m=-3或m=2（舍去），最后根据OE=4-3=1，可得E（1，0）．

解：(1)由题意得A(2，0)，B(0，4)，OA=2，

∵S△OAC=·OA·yc=6，∴yc=6．

∵点C在直线y=-2x+4上，

∴6=-2x+4，∴x=-1，∴点C的坐标为(-1，6)．

∵点C在双曲线y=(x<0)上，∴6=，解得k=-6．

∴双曲线的解析式为y=-．

（2）过点D作DF⊥x轴于F，过C作CG⊥DF于G，则∠G=∠DFE=90°，
由旋转可得，CD=DE，∠CDE=90°，

∴∠CDG=∠DEF，
在△DCG和△EDF中，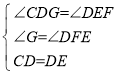
，
∴△DCG≌△EDF（AAS），
∴CG=DF，DG=EF，

设D的坐标为m，-，则DF=-，FO=-m，

∵C（-1，6），
∴CG=-1-a，
∴DF=-1-a，
∴-=-1-a，
解得a=-3或a=2（舍去），
∴DF=-1+3=2，DG=GF-DF=6-2=4，
∴EF=4，
又∵FO=3，
∴OE=4-3=1，

∴点E的坐标为(1，0)．