ƒøƒ⁄»›
°æƒø°øŒ™¡ÀÕ∆Ω¯«Ú¿‡‘À∂صƒ∑¢’𣨃≥–£◊È÷Ø–£ƒ⁄«Ú¿‡‘À∂ت·£¨∑÷¿∫«Ú°¢◊„«Ú°¢≈≈«Ú°¢”√´«Ú°¢∆π≈“«ÚŒÂœÓ£¨“™«Û√øŒª—ß…˙±ÿ–Î≤Œº”“ªœÓ≤¢«“÷ªƒ‹≤Œº”“ªœÓ£¨ƒ≥∞‡”–“ª√˚—ß…˙∏˘æ›◊‘º∫¡ÀΩ‚µƒ∞‡ƒ⁄«ÈøˆªÊ÷∆¡À»ÁÕºÀ˘ 浃≤ªÕÍ’˚Õ≥º∆±Ì∫Õ…»–ŒÕ≥º∆Õº.

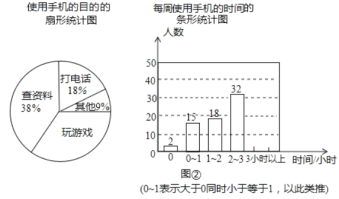
«Î∏˘æ›Õº±Ì÷–Ã·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©Õº±Ì÷–m=________£¨n=________£ª
£®2£©»Ù∏√–£—ß…˙π≤”–1000»À£¨‘Ú∏√–£≤Œº””√´«ÚªÓ∂صƒ»À ˝‘ºŒ™________»À£ª
£®3£©∏√∞‡≤Œº”∆π≈“«ÚªÓ∂صƒ4ŒªÕ¨—ß÷–£¨”–3Œªƒ–Õ¨—ߣ®∑÷±”√A£¨B£¨C±Ì 棩∫Õ1Œª≈ÆÕ¨—ߣ®”√D±Ì 棩£¨œ÷◊º±∏¥”÷–—°≥ˆ¡Ω√˚Õ¨—ß≤Œº”À´¥Ú±»»¸£¨”√ ˜◊¥ÕºªÚ¡–±Ì∑®«Û≥ˆ«°∫√—°≥ˆ“ªƒ–“ª≈Ƶƒ∏≈¬ .
°æ¥∞∏°ø£®1£©16£ª20£ª£®2£©150£ª£®3£©![]() .
.
°æΩ‚Œˆ°ø£®1£©∏˘æ›◊„«Úµƒ»À ˝∫Õ∞Ÿ∑÷±»£¨«Û≥ˆ◊‹»À ˝º¥ø…Ω‚æˆŒ £ª
£®2£©¿˚”√—˘±æπ¿º∆◊‹ÃµƒÀºœÎº¥ø…Ω‚æˆŒ £ª
£®3£©ª≠≥ˆ ˜◊¥Õº£¨∏˘æ›∏≈¬ π´ Ωº¥ø…«ÛΩ‚£Æ
£®1£©”…Õ≥º∆±Ì∫Õ…»–ŒÕ≥º∆Õºø…µ√£∫
◊„«Úµƒ»À ˝Œ™6»À£¨∞Ÿ∑÷±»Œ™15%£¨
°‡◊‹»À ˝Œ™6°¬15%=40£®»À£©£¨
°‡m=40°¡40%=16£®»À£©£¨
n%=8°¬40=20%.
°‡n=20.
£® 2 £©≤Œº””√´«ÚªÓ∂صƒ∞Ÿ∑÷±»Œ™£∫6°¬40=15%£¨
°‡∏√–£≤Œº””√´«ÚªÓ∂صƒ»À ˝Œ™£∫1000°¡15%=150£®»À£©.
¥£∫∏√–£≤Œº””√´«ÚªÓ∂صƒ»À ˝‘ºŒ™150»À.
£®3£©“¿Ã‚ø…µ√£∫

°‡¥”4»À÷–—°≥ˆ¡Ω√˚Õ¨—ßµƒÀ˘”–«Èøˆ”–12÷÷£¨∂¯“ªƒ–“ª≈Ƶƒ«Èøˆ”–6÷÷£¨
‘ÚP£®«°∫√—°µΩ“ªƒ–“ª≈Æ£©=![]() £Æ
£Æ

°æƒø°øŒ™¡ÀΩ‚ƒ≥«¯∞ÀƒÍº∂—ß…˙µƒÀØ√fl«Èøˆ£¨Àʪ˙≥È»°¡À∏√«¯∞ÀƒÍº∂—ß…˙≤ø∑÷—ß…˙Ω¯––µ˜≤È.“—÷™D◊ȵƒ—ß…˙”–15»À£¨¿˚”√≥È—˘À˘µ√µƒ ˝æ›ªÊ÷∆À˘ 浃Õ≥º∆Õº±Ì.
“ª°¢—ß…˙ÀØ√fl«Èøˆ∑÷◊ọ̇̄®µ•Œª£∫–° ±£©
◊ȱ | ÀØ√fl ±º‰ |
|
|
|
|
|
|
|
|
|
|
∂˛°¢—ß…˙ÀØ√fl«ÈøˆÕ≥º∆Õº
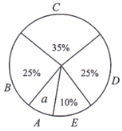
∏˘æ›Õº±ÌÃ·π©µƒ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
£®1£© ‘«Û°∞∞ÀƒÍº∂—ß…˙ÀØ√fl«ÈøˆÕ≥º∆Õº°±÷–µƒaµƒ÷µº∞a∂‘”¶µƒ…»–Œµƒ‘≤–ƒΩ«∂» ˝£ª
£®2£©»Áπ˚ÀØ√fl ±º‰x£® ±£©¬˙◊„£∫![]() £¨≥∆ÀØ√fl ±º‰∫œ∏Ò.“—÷™∏√«¯∞ÀƒÍº∂—ß…˙”–3250»À£¨ ‘π¿º∆∏√«¯∞ÀƒÍº∂—ß…˙ÀØ√fl ±º‰∫œ∏Òµƒπ≤”–∂‡…Ÿ»À£ø
£¨≥∆ÀØ√fl ±º‰∫œ∏Ò.“—÷™∏√«¯∞ÀƒÍº∂—ß…˙”–3250»À£¨ ‘π¿º∆∏√«¯∞ÀƒÍº∂—ß…˙ÀØ√fl ±º‰∫œ∏Òµƒπ≤”–∂‡…Ÿ»À£ø
£®3£©»Áπ˚Ω´∏˜◊ȱ—ß…˙ÀØ√fl«Èøˆ∑÷◊ȵƒ◊Ó–°÷µ£®»ÁC◊ȱ÷–£¨»°![]() £©£¨B°¢C°¢D»˝◊È—ß…˙µƒ∆Ωæ˘ÀØ√fl ±º‰◊˜Œ™∞ÀƒÍº∂—ß…˙µƒÀØ√fl ±º‰µƒ“¿æ›. ‘«Û∏√«¯∞ÀƒÍº∂—ß…˙µƒ∆Ωæ˘ÀØ√fl ±º‰.
£©£¨B°¢C°¢D»˝◊È—ß…˙µƒ∆Ωæ˘ÀØ√fl ±º‰◊˜Œ™∞ÀƒÍº∂—ß…˙µƒÀØ√fl ±º‰µƒ“¿æ›. ‘«Û∏√«¯∞ÀƒÍº∂—ß…˙µƒ∆Ωæ˘ÀØ√fl ±º‰.