题目内容
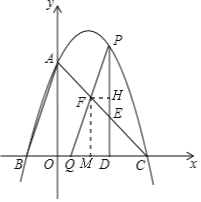
【题目】如图,已知抛物线经过 A、B、C 三点,其中 A(0,3),B(﹣1,0),且∠ACO=45°;
(1)求抛物解析式;
(2)点 P 为线段 AC 上方抛物线上一动点,过 P 作 PQ∥AB 分别交 AC、x 轴于 F、Q 两点, 过 P 作 PD⊥x 轴分别交 AC、x 轴于 E、D 两点,且 S△CFQ=3S△PEF;①![]() 的值;②求 F 点坐标.
的值;②求 F 点坐标.

【答案】(1)![]() ;(2)①1,②
;(2)①1,② ![]()
【解析】
(1)根据已知条件可得:![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 的坐标为
的坐标为![]() ,将抛物线的解析式设为
,将抛物线的解析式设为![]() ,然后将点
,然后将点![]() 代入求得
代入求得![]() 即可;
即可;
(2)过点![]() 作
作![]() ,
,![]() ,设
,设![]() ,利用面积关系和三角形相似建立方程,求得
,利用面积关系和三角形相似建立方程,求得![]() 的值;
的值;
(3)设点![]() 坐标,用
坐标,用![]() 与
与![]() 的相似比表示线段长度,求得点
的相似比表示线段长度,求得点![]() 的坐标,代入解析式即可求得
的坐标,代入解析式即可求得![]() 点的坐标;
点的坐标;
解:(1)∵![]()
∴![]()
∴点![]() 坐标为
坐标为![]()
设抛物线的解析式为:![]()
将![]() 代入可得:
代入可得:![]()
![]() 抛物线的解析式为:
抛物线的解析式为:![]()
(2)如图,过点![]() 作
作![]()
设![]()
![]()
![]()
![]()
![]()
![]()
![]() 轴
轴
![]()
![]()
![]()
![]()
![]()
![]()
![]()
可得![]() ,
,
![]() ,
,![]()
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
∵![]()
![]()
![]()
![]()
![]()
![]()
(3)![]()
![]() 的直线解析式为:
的直线解析式为:![]()
设 ![]() ,则
,则![]()
![]()
![]()
![]()
由①得:![]()
![]()
![]()
![]()
![]()
将点![]() 坐标代入解析式
坐标代入解析式 ![]() 中可得:
中可得: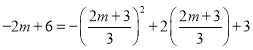
解得![]() (舍)
(舍)
![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
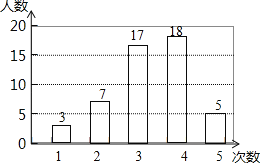
二、学生睡眠情况统计图
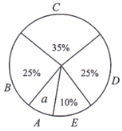
根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.