题目内容
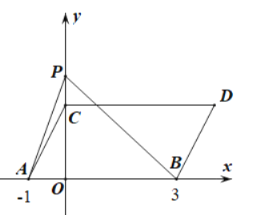
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(![]() ,0),(3,0).现将线段AB向上平移2个单位,再向右平移1个单位,得到线段AB的对应线段CD,连接AC,BD.
,0),(3,0).现将线段AB向上平移2个单位,再向右平移1个单位,得到线段AB的对应线段CD,连接AC,BD.
(1)点C,D的坐标分别为_______, ________,并求出四边形ABDC的面积S四边形ABDC;
(2)在y轴上存在一点P,连接PA,PB,且S△PAB =S四边形ABDC,求出满足条件的所有点P的坐标.
(3)若点Q为线段BD上一点(不与B,D两点重合),则![]() 的值______(填“变”或“不变”).
的值______(填“变”或“不变”).

【答案】(1)C(0,2),D(4,2),8;(2)P(0,4)或P(0,-4);(3)不变
【解析】
(1)根据平移的特点可得出点C、D的坐标,利用平行四边形的面积公式可求面积;
(2)存在2种情况,点P在y轴正半轴和点P在y轴负半轴,另△ABP的面积与平行四边形ABDC面积相等可求得点P的坐标;
(3)如下图,利用平行的性质可求得∠CQO=∠DCQ+∠QOB,可得不变关系.
解:(1)∵将线段AB向上平移2个单位,再向右平移1个单位得到点C、D
又∵点A,B的坐标分别为(![]() ,0),(3,0)
,0),(3,0)
∴C(0,2),D(4,2).
由题意可知:四边形ABDC为平行四边形,
∴S四边形ABDC=OC×AB=2×4=8.
(2)当点P在y轴正半轴时,设点P的纵坐标为a,图形如下
根据题意,得![]() ×4=8.
×4=8.
解得:a=4
同理当点P在y轴负半轴时,a=-4
∴P(0,4)或P(0,-4).
(3)不变.
图形如下,过点Q作QM∥CD

∵CD是AB平移得到,∴AB∥CD
∵QM∥CD,∴QM∥AB
∴∠DCQ=∠CQM,∠MQO=∠QOB
∴∠DCQ+∠QOB=∠CQM+∠MQO=∠CQO
∴![]() ,比值始终不变
,比值始终不变

练习册系列答案
相关题目





