题目内容
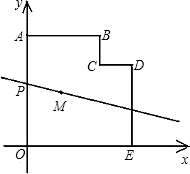
如图,在平面直角坐标系xOY中,多边形OABCDE的顶点坐标分别是
O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).
若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,求直线l的函数表达式.
O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).
若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,求直线l的函数表达式.

如图,延长BC交x轴于点F,连接OB,AF,DF,CE,DF和CE相交于点N,
∵O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).
∴四边形OABF为矩形,四边形CDEF为矩形,
∴点M(2,3)是矩形OABF对角线的交点,即点M为矩形ABFO的中心,
∴直线l把矩形ABFO分成面积相等的两部分
又∵点N(5,2)是矩形CDEF的中心,
∴过点N(5,2)的直线把矩形CDEF分成面积相等的两部分.
∴直线MN即为所求的直线L,
设直线l的解析式为y=kx+b,
则2k+b=3,5k+b=2,
解得k=-
,b=
,
因此所求直线l的函数表达式是:y=-
x+
.

∵O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).
∴四边形OABF为矩形,四边形CDEF为矩形,
∴点M(2,3)是矩形OABF对角线的交点,即点M为矩形ABFO的中心,
∴直线l把矩形ABFO分成面积相等的两部分
又∵点N(5,2)是矩形CDEF的中心,
∴过点N(5,2)的直线把矩形CDEF分成面积相等的两部分.
∴直线MN即为所求的直线L,
设直线l的解析式为y=kx+b,
则2k+b=3,5k+b=2,
解得k=-
| 1 |
| 3 |
| 11 |
| 3 |
因此所求直线l的函数表达式是:y=-
| 1 |
| 3 |
| 11 |
| 3 |


练习册系列答案
相关题目
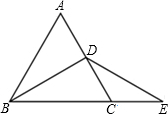 三个为条件,余下l一个为结论,组成一个正确l命题(只需写出一种),并给予证明.
三个为条件,余下l一个为结论,组成一个正确l命题(只需写出一种),并给予证明.