Question

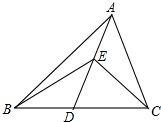
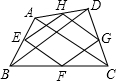
如图，已知凸四边形ABCD的两对角线BD与AC之比为k，菱形EFGH各顶点位于四边形ABCD的顺次四边之上，且EF∥AC，FG∥BD，则四边形ABCD与菱形EFGH的面积之比为______．

Answer 1

设

AE

AB

=a，则

BE

AB

=1-a，

EH

BD

=a，EH=a•BD，
同理：EF=（1-a）•AC，
∵菱形EFGH，
∴EF=EH，
∴a•BD=（I-a）•AC，
∴

BD

AC

=

1-a

a

，
∵

BD

AC

=k，
∴a=

1

k+1

，
由面积公式得：

S四边形ABCD

S菱形EFGH

=

1 2 AC•BD•sina

EF•EH•sina

，
=

AC•BD

2EF•EH

，
=

1

2

•

1

1-a

•

1

a

，
=

1

2

•

1

1- 1 k+1

•（k+1），
=

(k+1)2

2k

．
故答案为：

(k+1)2

2k

．