题目内容
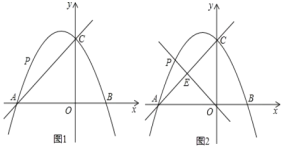
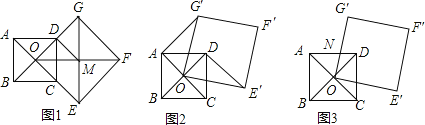
【题目】如图,点O是正方形ABCD两条对角线的交点,分别延长CO到点G,OC到点E,使OG=2OD、OE=2OC,然后以OG、OE为邻边作正方形OEFG.
(1)如图1,若正方形OEFG的对角线交点为M,求证:四边形CDME是平行四边形.
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转,得到正方形OE′F′G′,如图2,连接AG′,DE′,求证:AG′=DE′,AG′⊥DE′;
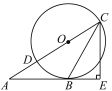
(3)在(2)的条件下,正方形OE′F′G′的边OG′与正方形ABCD的边相交于点N,如图3,设旋转角为α(0°<α<180°),若△AON是等腰三角形,请直接写出α的值.
【答案】(1)证明见解析;(2)证明见解析;(3)α的值是22.5°或45°或112.5°或135°或157.5°.
【解析】
(1)由四边形OEFG是正方形,得到ME=![]() GE,根据三角形的中位线的性质得到CD∥GE,CD=
GE,根据三角形的中位线的性质得到CD∥GE,CD=![]() GE,求得CD=GE,即可得到结论;
GE,求得CD=GE,即可得到结论;
(2)如图2,延长E′D交AG′于H,由四边形ABCD是正方形,得到AO=OD,∠AOD=∠COD=90°,由四边形OEFG是正方形,得到OG′=OE′,∠E′OG′=90°,由旋转的性质得到∠G′OD=∠E′OC,求得∠AOG′=∠COE′,根据全等三角形的性质得到AG′=DE′,∠AG′O=∠DE′O,即可得到结论;
(3)分类讨论,根据三角形的外角的性质和等腰三角形的性质即可得到结论.
(1)证明:∵四边形OEFG是正方形,
∴ME=![]() GE,
GE,
∵OG=2OD、OE=2OC,
∴CD∥GE,CD=![]() GE,
GE,
∴CD=GE,
∴四边形CDME是平行四边形;
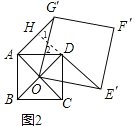
(2)证明:如图2,延长E′D交AG′于H,
∵四边形ABCD是正方形,
∴AO=OD,∠AOD=∠COD=90°,
∵四边形OEFG是正方形,
∴OG′=OE′,∠E′OG′=90°,
∵将正方形OEFG绕点O逆时针旋转,得到正方形OE′F′G′,
∴∠G′OD=∠E′OC,
∴∠AOG′=∠COE′,
在△AG′O与△ODE′中,
 ,
,
∴△AG′O≌△ODE′
∴AG′=DE′,∠AG′O=∠DE′O,
∵∠1=∠2,
∴∠G′HD=∠G′OE′=90°,
∴AG′⊥DE′;
(3)①正方形OE′F′G′的边OG′与正方形ABCD的边AD相交于点N,如图3,
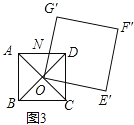
Ⅰ、当AN=AO时,
∵∠OAN=45°,
∴∠ANO=∠AON=67.5°,
∵∠ADO=45°,
∴α=∠ANO-∠ADO=22.5°;
Ⅱ、当AN=ON时,
∴∠NAO=∠AON=45°,
∴∠ANO=90°,
∴α=90°-45°=45°;
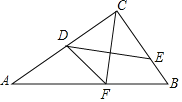
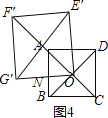
②正方形OE′F′G′的边OG′与正方形ABCD的边AB相交于点N,如图4,
Ⅰ、当AN=AO时,
∵∠OAN=45°,
∴∠ANO=∠AON=67.5°,
∵∠ADO=45°,
∴α=∠ANO+90°=112.5°;
Ⅱ、当AN=ON时,
∴∠NAO=∠AON=45°,
∴∠ANO=90°,
∴α=90°+45°=135°,
Ⅲ、当AN=AO时,旋转角a=∠ANO+90°=67.5+90=157.5°,
综上所述:若△AON是等腰三角形时,α的值是22.5°或45°或112.5°或135°或157.5°.

【题目】某校准备开设特色活动课,各科目的计划招生人数和报名人数,列前三位的如下表所示:
科目 | 小制作 | 足球 | 英语口语 |
计划人数 | 100 | 90 | 60 |
科目 | 小制作 | 英语口语 | 中国象棋 |
报名人数 | 280 | 250 | 200 |
若计划招生人数和报名人数的比值越大,表示学校开设该科目相对学生需要的满足指数就越高.那么根据以上数据,满足指数最高的科目是( )
A. 足球B. 小制作C. 英语口语D. 中国象棋