题目内容
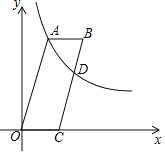
【题目】如图，在平面直角坐标系中，OABC的顶点C在x轴上，函数y=
（k＞0，x＞0）的图象经过点A（2，6），且与边BC交于点D．若点D是边BC的中点，则OC的长为（ ）
A. 2B. 2.5C. 3.5D. 3
【答案】D
【解析】
设OC的长为x，则C（x，0）．根据平行四边形的性质以及A点坐标为（2，6），得出B（2+x，6），由点D是边BC的中点，利用线段的中点坐标公式得出D（1+x，3），再根据函数y=
（k＞0，x＞0）的图象经过点A（2，6），D，利用反比例函数图象上点的坐标特征得出3（1+x）=2×6，解方程即可．
设OC的长为x，则C（x，0）．
∵四边形OABC是平行四边形，
∴AB∥OC，AB=OC=x，
∵A（2，6），
∴B（2+x，6），
∵点D是边BC的中点，
∴D（1+x，3），
∵函数y=（k＞0，x＞0）的图象经过点A（2，6），D，
∴3（1+x）=2×6，
∴x=3．
故选D．
智慧小复习系列答案
【题目】现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）：
步数 | 频数 | 频率 |
0≤x＜4000 | 8 | a |
4000≤x＜8000 | 15 | 0.3 |
8000≤x＜12000 | 12 | b |
12000≤x＜16000 | c | 0.2 |
16000≤x＜20000 | 3 | 0.06 |
20000≤x＜24000 | d | 0.04 |
请根据以上信息，解答下列问题：
（1）写出a，b，c，d的值并补全频数分布直方图；
（2）本市约有37800名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？
（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步的两名教师与大家分享心得，求被选取的两名教师恰好都在20000步（包含20000步）以上的概率．
【题目】某游泳馆每年夏季推出两种游泳付费方式．方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费4元；方式二：不购买会员证，每次游泳付费10元．设小明计划今年夏季游泳次数为x（x为正整数）．
(1)根据题意，填写下表：
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用（元） | 140 | 160 | _______ | … | _______ |
方式二的总费用（元） | 100 | 150 | ________ | … | ________ |
(2)若小明计划今年夏季游泳的总费用为260元，选择哪种付费方式，他游泳的次数比较多？
(3)小明选择哪种付费方式更合算？并说明理由．
【题目】在水果销售旺季，某水果店购进一优质水果，进价为20元/千克，售价不低于20元/千克，且不超过32元/千克，根据销售情况，发现该水果一天的销售量y（千克）与该天的售价x（元/千克）满足如下表所示的一次函数关系．
销售量y（千克） | … | 34.8 | 32 | 29.6 | 28 | … |
售价x（元/千克） | … | 22.6 | 24 | 25.2 | 26 | … |
（1）某天这种水果的售价为23.5元/千克，求当天该水果的销售量．
（2）如果某天销售这种水果获利150元，那么该天水果的售价为多少元？