Question

【题目】已知正方形，为射线上的一点，以为边作正方形，使点在线段的延长线上，连接

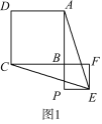
(1)如图，若点在线段的延长线上，求证：；

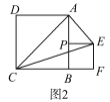
(2)如图，若点在线段的中点，连接，判断的形状，并说明理由；

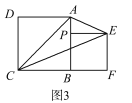
(3)如图，若点在边上，连接，当平分时，设，求度数.

Answer 1

【答案】(1)证明见解析；(2)△ACE是直角三角形；(3)

【解析】

（1）根据正方形的性质证明△APE≌△CFE，可得结论；

（2）分别证明∠PAE=45°和∠BAC=45°，则∠CAE=90°，即△ACE是直角三角形；

（3）分别计算PG和BG的长，再计算GH和BG的长，根据角平分线的逆定理得：∠HCG=∠BCG，由平行线的性质得到∠AEC=∠ACB=45°．

解：(1)∵四边形和四边形是正方形，

，

∵

，

(2)是直角三角形

∵为的中点

又∵

又∵

，即是直角三角形

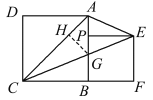
(3)如图，设交于点，

∵平分,

，

作

又∵

又∵

∵