题目内容
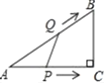
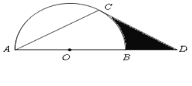
【题目】如图,已知四边形![]() 为矩形,点
为矩形,点![]() 在
在![]() 上(不与
上(不与![]() ,
,![]() 重合),连接
重合),连接![]() ,
,![]() ,以
,以![]() 为一边作正方形
为一边作正方形![]() ,使得点
,使得点![]() 在边
在边![]() 上,给出以下结论:①
上,给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
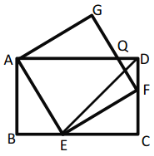
A.1个B.2个C.3个D.4个
【答案】D
【解析】
利用AAS得到△ABE≌△ECF可判断①正确;利用等量代换可判断③正确;证得![]() ,
,![]() ,可判断②正确;可求得∠ADE=45°,∠AQG
,可判断②正确;可求得∠ADE=45°,∠AQG![]() 45
45![]() ,可判断④错误;证得△EFC
,可判断④错误;证得△EFC![]() △AQG,利用等量代换可判断⑤正确.
△AQG,利用等量代换可判断⑤正确.
∵四边形AEFG为正方形,四边形ABCD为矩形,如图:
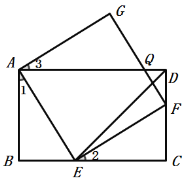
∴∠AEF=∠B=∠C=90°,AE=EF,AB=CD,
∴∠1+∠AEB=90°,∠2+∠AEB =90°,
∴∠1=∠2,
在△ABE和△ECF中,
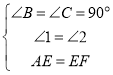 ,
,
∴△ABE≌△ECF(AAS),故①正确;
∴BE=CF,AB=EC,
∴BC+DF= BE+EC+DF = CF+EC+DF= CD+EC= AB+EC=2 EC,故③正确;
∵![]() ,
,
![]() ,
,
∴![]() ,故②正确;
,故②正确;
∵CD= AB=EC,
∴∠CED=∠CDE=∠ADE=45°,
∵∠1+∠EAD=90°,∠3+∠EAD=90°,
∴∠1=∠3,
∵∠AQG=90°-∠3=90°-∠1=90°-∠2,且∠2![]() 45
45![]() ,
,
∴∠AQG![]() 45
45![]() ,
,
∴∠ADE![]() ∠AQG,故④错误;
∠AQG,故④错误;
∵四边形AEFG为正方形,
∴∠G=90°,AG=EF,
∵∠1=∠2=∠3,
∴Rt△EFC![]() Rt△AQG,
Rt△AQG,
∴![]() ,
,
∴![]() ,故⑤正确;
,故⑤正确;
综上,①②③⑤正确,共4个.
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目