题目内容
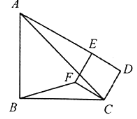
【题目】感知:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=m,将边AB绕点B顺时针旋转90°得到线段BD,过点D作DE⊥CB交CB的延长线于点E,连接CD.
(1)求证:△ACB≌△BED;
(2)△BCD的面积为 (用含m的式子表示).
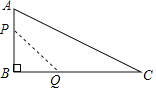
拓展:如图②,在一般的Rt△ABC,∠ACB=90°,BC=m,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,用含m的式子表示△BCD的面积,并说明理由.
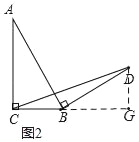
应用:如图③,在等腰△ABC中,AB=AC,BC=8,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,则△BCD的面积为 ;若BC=m,则△BCD的面积为 (用含m的式子表示).

【答案】感知:(1)详见解析;(2)![]() m2;拓展:
m2;拓展: ![]() m2,理由详见解析;应用:16,
m2,理由详见解析;应用:16, ![]() m2.
m2.
【解析】
感知:(1)由题意可得CA=CB,∠A=∠ABC=45°,由旋转的性质可得BA=BD,∠ABD=90°,可得∠DBE=∠ABC,即可证△ACB≌△BED;
(2)由△ACB≌△BED,可得BC=DE=m,根据三角形面积求法可求△BCD的面积;
拓展:作DG⊥CB交CB的延长线于G,可证△ACB≌△BGD,可得BC=DG=m,根据三角形面积求法可求△BCD的面积;
应用:过点A作AN⊥BC于N,过点D作DM⊥BC的延长线于点M,由等腰三角形的性质可以得出BN=![]() BC,由条件可以得出△AFB≌△BED就可以得出BN=DM,由三角形的面积公式就可以得出结论.
BC,由条件可以得出△AFB≌△BED就可以得出BN=DM,由三角形的面积公式就可以得出结论.
感知:证明:(1)∵△ABC是等腰直角三角形,
∴CA=CB=m,∠A=∠ABC=45°,
由旋转的性质可知,BA=BD,∠ABD=90°,
∴∠DBE=45°,
在△ACB和△DEB中,
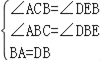 ,
,
∴△ACB≌△BED(AAS)
(2)∵△ACB≌△BED
∴DE=BC=m
∴S△BCD=![]() BC×ED=
BC×ED=![]() m2,
m2,
故答案为![]() m2,
m2,
拓展:作DG⊥CB交CB的延长线于G,
∵∠ABD=90°,
∴∠ABC+∠DBG=90°,又∠ABC+∠A=90°,
∴∠A=∠DBG,
在△ACB和△BGD中,
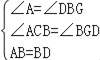 ,
,
∴△ACB≌△BGD(AAS),
∴BC=DG=m
∴S△BCD=![]() BC×DG=
BC×DG=![]() m2,
m2,
应用:作AN⊥BC于N,DM⊥BC交CB的延长线于M,

∴∠ANB=∠M=90°,BN=![]() BC=4.
BC=4.
∴∠NAB+∠ABN=90°.
∵∠ABD=90°,
∴∠ABN+∠DBM=90°,
∴∠NAB=∠MBD.
∵线段BD是由线段AB旋转得到的,
∴AB=BD.
在△AFB和△BED中,
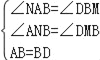 ,
,
∴△ANB≌△BMD(AAS),
∴BN=DM=![]() BC=4.
BC=4.
∴S△BCD=![]() BCDM=
BCDM=![]() ×8×4=16,
×8×4=16,
若BC=m,则BN=DM=![]() BC=
BC=![]() m,
m,
∴S△BCD=![]() BCDM=
BCDM=![]() ×m×
×m×![]() m=
m=![]() m2
m2
故答案为16,![]() m2.
m2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
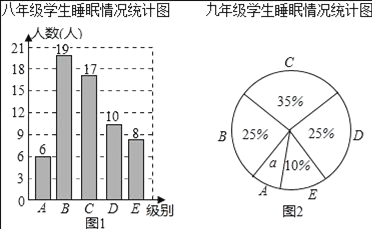
小学生10分钟应用题系列答案【题目】为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
组别 | 睡眠时间x(小时) |
|
|
|
|
|
|
|
|
|
|
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中![]() 的值 ;
的值 ;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?