Question

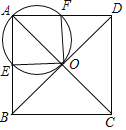
【题目】已知，如图，正方形ABCD的对角线AC，BD相交于点O，点E为AB上一点（不与A．B两点重合），过点O，A，E的⊙I交AD于F，AB＝5

（1）求⊙I的直径的取值范围；

（2）若⊙I的半径为2，求AE的长．

Answer 1

【答案】(1)⊙I的直径＜5;(2).

【解析】

（1）当OE⊥AB时，⊙I的直径值最小，当OB⊥AO时，⊙I的直径值最大；

（2）分两种情况讨论，当点E和点I在AO同侧，过点I作IF⊥AO，过点O作OH⊥AB，解直角三角形求AH和HE即可.

当点E和点I在AO异侧，过点I作IF⊥AO，过点O作OH⊥AB, 解直角三角形求AH和HE即可.

解：（1）∵四边形ABCD是正方形

∴AB＝BC＝5，AC＝BD，AO＝CO＝BO＝DO，AC⊥BD，∠BAC＝45°，

∴AC＝BD＝5，AO＝BO

当OE⊥AB时，⊙I的直径的最小值为

当点B与点E重合，即OE⊥OA时，⊙I的直径的最小值为5

∴⊙I的直径＜5

（2）当点E和点I在AO同侧，如图，过点I作IF⊥AO，过点O作OH⊥AB

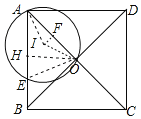
∵OH⊥AB，∠BAO＝45°

∴AH＝HO

∵IF⊥AO

∴AF＝FOAO，∠AIO＝2∠AIF

∴IF

∵∠AIO＝2∠AEO

∴∠AEO＝∠AIF

∴tan∠AEO＝tan∠AIF

∴

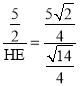
∴HE

∴AE＝AH+HE

当点E和点I在AO异侧，如图，过点I作IF⊥AO，过点O作OH⊥AB

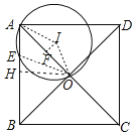
同理可求AH，HE

∴AE