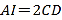题目内容
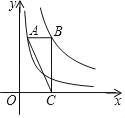
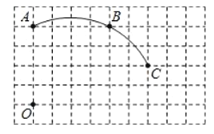
【题目】如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点![]() 、
、![]() 、
、![]() .
.
(1)请完成如下操作:①以点![]() 为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;②根据图形提供的信息,标出该圆弧所在圆的圆心
为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;②根据图形提供的信息,标出该圆弧所在圆的圆心![]() ,并连接
,并连接![]() 、
、![]() .
.
(2)请在(1)的基础上,完成下列填空:
①写出圆心点![]() 的坐标:( , );
的坐标:( , );
②![]() 的半径= (结果保留根号);
的半径= (结果保留根号);
③若扇形![]() 是一个圆锥的侧面展开图,则该圆锥的底面的面积为 ;(结果保留
是一个圆锥的侧面展开图,则该圆锥的底面的面积为 ;(结果保留![]() )
)
【答案】①点![]() .②
.②![]() 的半径
的半径![]() ;③该圆锥的底面的面积为
;③该圆锥的底面的面积为![]() .
.
【解析】
①利用过三点的圆可得圆心为圆上任意两条弦的垂直平分线的交点,即可得到D.
②利用勾股定理即可求出![]() 的半径.
的半径.
③先求出扇形的弧长即为圆锥的底面圆的周长,即可算出底面圆的半径,从而可求出底面圆的面积.
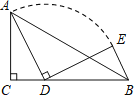
①根据圆心为弦垂直平分线的交点,故分别作AB、BC的中垂线交点即为D,
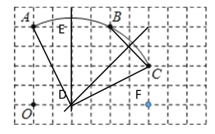
由图可知作点![]() .
.
②连接AD即为半径,在Rt三角形AED中
![]() 的半径
的半径![]() .
.
③由图可知,OA=DF=4,∠AOD=∠DFC=90°,OD=CF=2
∴△AOD≌△DFC
∴∠ADO=∠DCF,
又∵∠DCF+∠CDF=90°
∴∠ADO+∠CDF=90°
∴∠ADC=90°
∴![]()
根据圆锥侧面弧长等于底面圆的周长,
所以该圆锥的底面的半径为![]() .
.
该圆锥的底面的面积为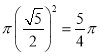

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目