��Ŀ����
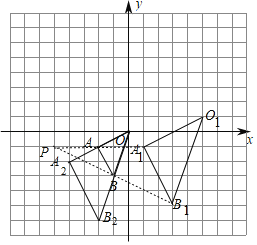
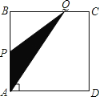
����Ŀ������ͼ��ʾ�ķ����У���OAB�Ķ�������ֱ�ΪO��0��0����A����2����1����B����1����3������O1A1B1���OAB�ǹ��ڵ�PΪλ�����ĵ�λ��ͼ�Σ�
��1����ͼ�б��λ������P��λ�ã���д����P�����꼰��O1A1B1���OAB�����Ʊȣ�
��2����ԭ��OΪλ�����ģ���y���������OAB����һ��λ�ơ�OA2B2��ʹ�����OAB�����Ʊ�Ϊ2��1����д����B�Ķ�Ӧ��B2�����꣮
��3����OA2B2��������� ����
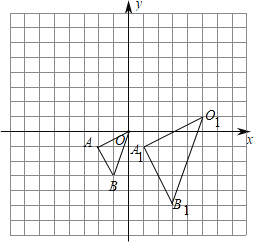
���𰸡���1����ͼ��������P������Ϊ����5����1������O1A1B1���OAB�����Ʊ�Ϊ2����2����ͼ����������B2������Ϊ����2����6������3��10��
��������
��1���ӳ�B1B��A1A�����ǵĽ��㼴ΪP�㣬��һ���������P�����꼰��O1A1B1���OAB�����Ʊ���
��2���ӳ�OA��A2��ʹOA2��2OA���ӳ�OB��B2��ʹOB2��2OB�����OA2B2����������
��3�����ж���OA2B2����״����һ��������ý����
�⣺��1����ͼ��ʾ������B1B��A1A���ӳ������ǵĽ��㼴ΪP�㣻 P������Ϊ����5����1������O1A1B1���OAB�����Ʊȣ�![]() ��2��
��2��
��2����ͼ��ʾ����OA2B2Ϊ��������B2������Ϊ����2����6����
��3����![]() ����
����![]() ��
��
��![]() �ǵ���ֱ�������Σ����OA2B2�����Ϊ��
�ǵ���ֱ�������Σ����OA2B2�����Ϊ��![]() ��2
��2![]() ��2
��2![]() ��10��
��10��
�ʴ�Ϊ��10��