题目内容
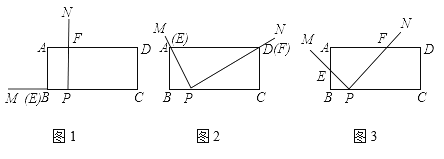
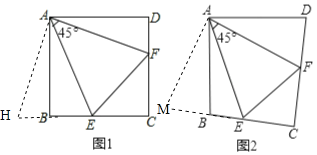
【题目】(1)如图 1,已知正方形 ABCD,点 E 在 BC 上,点 F 在 DC 上,且∠EAF=45°,则有 BE+DF= .若 AB=4,则△CEF 的周长为 .
(2)如图 2,四边形 ABCD 中,∠BAD=∠C=90°,AB=AD,点 E,F 分别在 BC,CD 上,且∠EAF=45°,试判断 BE,EF,DF 之间的数量关系,并说明理由.

【答案】(1)EF,8;(2)EF=BE+DF.
【解析】
(1)延长EB至H,使BH=DF,连接AH,证△ADF≌△ABH,△FAE≌△HAE,根据全等三角形的性质得出EF=HE=BE+HB进而求出即可;
(2)延长CB至M,使BM=DF,连接AM,证△ADF≌△ABM,证△FAE≌△MAE,即可得出答案.
(1)延长EB至H,使BH=DF,连接AH,如图1,
∵在正方形ABCD中,
∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,
∵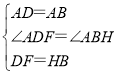 ,
,
∴△ADF≌△ABH(SAS),
∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,
∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,
∵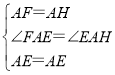 ,
,
∴△FAE≌△HAE(SAS),
∴EF=HE=BE+HB,
∴EF=BE+DF,
∴△CEF的周长=EF+CE+CF=BE+CE+DF+CF=BC+CD=2AB=8.
(2)延长CB至M,使BM=DF,连接AM,如图2,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
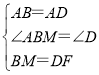 ,
,
∴△ABM≌△ADF(SAS),
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=∠C=90°,∠EAF=45°,
即∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
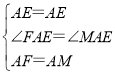 ,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.

 名校课堂系列答案
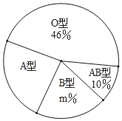
名校课堂系列答案【题目】“只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、AB、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):
血型统计表
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)本次随机抽取献血者人数为 人,图中m= ;
(2)补全表中的数据;
(3)若这次活动中该校有1300人义务献血,估计大约有多少人是A型血?
(4)现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.
【题目】小田同学学习反比例函数![]() 的图象和性质后,对新函数
的图象和性质后,对新函数![]() 的图象和性质进行了探究,以下是她的探究过程:.
的图象和性质进行了探究,以下是她的探究过程:.
第一步:在直角坐标系中,作出函数![]() 的图象;
的图象;
第二步:通过列表、描点、连线,作出新函数![]() 的图象
的图象
①列表:
| … | -4 | -2 | -1 | 0 | 1 | 3 | 4 | 5 | 6 | … |
| … | 1 | 1.5 | 2 | 3 | 6 | -6 | -3 | -2 | -1.5 | … |
②描点:如图所示.

(1)请在图中,帮助小田同学完成连线的步骤;
(2)观察图象,发现函数![]() 与函数
与函数![]() 的图象都是双曲线,并且形状也相同,只是位置发生了改变,由此可知,函数
的图象都是双曲线,并且形状也相同,只是位置发生了改变,由此可知,函数![]() 的图象可由函数
的图象可由函数![]() 的图象平移得到,请写出函数
的图象平移得到,请写出函数![]() 的图象是怎样平移得到的?
的图象是怎样平移得到的?
(3)若点![]() ,
,![]() 在函数图象
在函数图象![]() 上,且
上,且![]() ,则
,则![]()
![]() (选填“>”“<”或“=”)
(选填“>”“<”或“=”)