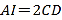题目内容
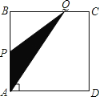
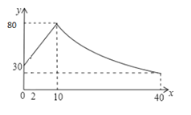
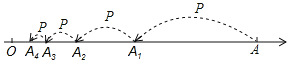
【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系
(1)求水柱所在抛物线(第一象限部分)的函数解析式
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿？
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度
【答案】（1）
；（2）为了不被淋湿，身高1.8米的人站立时必须在离水池中心7米以内；（3）
【解析】
（1）根据顶点坐标可设二次函数的顶点式，代入（8,0）即可求得a，此题得解；
（2）利用二次函数图象上点的坐标特征，求出当y=1.8时x的值，由此即可得出结论；
（3）利用二次函数图象上点的坐标特征可求出抛物线与y轴交点坐标，由抛物线的形状不变可设扩建后水柱所在抛物线（第一象限部分）的函数表达式为
，代入点（16,0）可求出b的值，再利用配方法将二次函数表达式变形为顶点式，即可得出结论.
（1）解：设水柱所在抛物线（第一象限部分）的函数表达式为
将（8，0）代入
，得：
25a+5=0
解得：
∴水柱所在抛物线（第一象限部分）的函数表达式为
（2）解：当
时，有
解得：
∴为了不被淋湿，身高1.8米的人站立时必须在离水池中心7米以内.
（3）解：当x=0时，
设扩建后水柱所在抛物线（第一象限部分）的函数表达式为
∵该函数图象经过点（16,0）
∴
解得：
∴扩建后水柱所在抛物线（第一象限部分）的函数表达式为
∴扩建后喷水池水柱的最大高度为
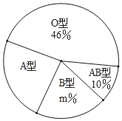
【题目】“只要人人献出一点爱，世界将变成美好的人间”．某大学利用“世界献血日”开展自愿义务献血活动，经过检测，献血者血型有“A、B、AB、O”四种类型，随机抽取部分献血结果进行统计，根据结果制作了如图两幅不完整统计图表（表，图）：
血型统计表
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
（1）本次随机抽取献血者人数为 人，图中m＝ ；
（2）补全表中的数据；
（3）若这次活动中该校有1300人义务献血，估计大约有多少人是A型血？
（4）现有4个自愿献血者，2人为O型，1人为A型，1人为B型，若在4人中随机挑选2人，利用树状图或列表法求两人血型均为O型的概率．
【题目】小田同学学习反比例函数
的图象和性质后，对新函数
的图象和性质进行了探究，以下是她的探究过程：.
第一步：在直角坐标系中，作出函数的图象；
第二步：通过列表、描点、连线，作出新函数的图象
①列表：
| … | -4 | -2 | -1 | 0 | 1 | 3 | 4 | 5 | 6 | … |
| … | 1 | 1.5 | 2 | 3 | 6 | -6 | -3 | -2 | -1.5 | … |
②描点：如图所示.
（1）请在图中，帮助小田同学完成连线的步骤；
（2）观察图象，发现函数与函数的图象都是双曲线，并且形状也相同，只是位置发生了改变，由此可知，函数的图象可由函数的图象平移得到，请写出函数的图象是怎样平移得到的？
（3）若点
，
在函数图象上，且
，则
（选填“>”“<”或“=”）
