题目内容
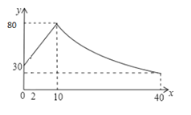
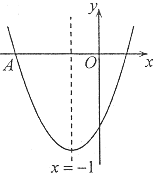
【题目】已知二次函数y=ax2+bx+c(a<0,b,c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④3b>2c;⑤a+b>m(am+b)(m为常数,且m≠1),其中正确的结论有_____.

【答案】①③④⑤
【解析】
根据抛物线开口方向可以判定a的符号,根据对称轴位置和a的符号可以确定b的符号,根据抛物线与y轴交点可确定c的符号,根据韦达定理可确定a与b和a与c的关系,根据二次函数图象与各项系数关系进行解答即可.
解:由图象可得,
a<0,b>0,c>0,
∴abc<0,故①正确,
当x=﹣1时,y=a﹣b+c<0,则b>a+c,故②错误,
∵对称轴为直线x=1,
∴x=0时和x=2时的函数值相等,当x=2时,y=4a+2b+c>0,故③正确,
∵![]() 1,则b=﹣2a,
1,则b=﹣2a,
∵x=﹣1时,y=a﹣b+c<0,
∴2a﹣2b+2c<0,故﹣3b+2c<0,
∴3b>2c,故④正确,
∵当x=1时,此函数取得最大值,此时y=a+b+c=1,
∴当x=m≠1时,am2+bm+c<a+b+c,
∴m(am+b)<a+b,故⑤正确,
故答案为:①③④⑤.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】“只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、AB、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):
血型统计表
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)本次随机抽取献血者人数为 人,图中m= ;
(2)补全表中的数据;
(3)若这次活动中该校有1300人义务献血,估计大约有多少人是A型血?
(4)现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.