题目内容
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
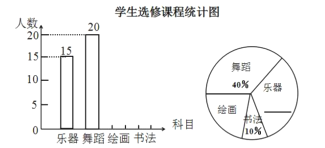
(1)补全条形统计图,补全扇形统计图中乐器所占的百分比;
(2)本次调查学生选修课程的“众数”是__________;
(3)若该校有1200名学生,请估计选修绘画的学生大约有多少名?
【答案】(1)详见解析;(2)舞蹈;(3)240
【解析】
(1)由舞蹈人数及其所占百分比求得总人数,总人数乘以书法对应百分比可求得其人数,依据各科目人数之和等于总人数求得绘画人数,再用乐器人数除以总人数可得其对应百分比.
(2)根据众数的定义求解即可.
(3)用总人数乘以样本中绘画对应的比例即可求解.
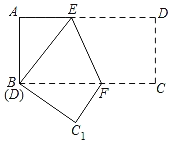
解:(1)被调查的总人数为:20÷40%=50(人),
∴书法的人数为:50×10%=5人,绘画的人数为:50-15-20-5=10(人),
则乐器所在的百分比为:15÷50×100%=30%,
补全统计图如图所示:
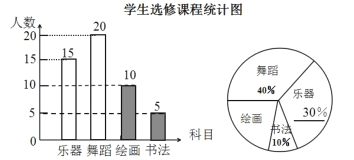
(2)本次调查学生选修课程的“众数”是舞蹈;
故答案为:舞蹈.
(3)选修绘画的人数占总人数的百分比为:![]() ,
,
所以估计选修绘画的学生大约有:![]() (人);
(人);
故答案为:240人.

 步步高达标卷系列答案
步步高达标卷系列答案【题目】某运输公司现将一批152吨的货物运往A,B两地,若用大小货车15辆,则恰好能一次性运完这批货.已知这两种大小货车的载货能力分别为12吨/辆和8吨/辆,其运往A,B两地的运费如下表所示:
目的地(车型) | A地(元/辆) | B地(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆.(用二元一次方程组解答)
(2)现安排其中的10辆货车前往A地,其余货车前往B地,设前往A地的大货车为x辆,前往A,B两地总费用为w元,试求w与x的函数解析式.