题目内容
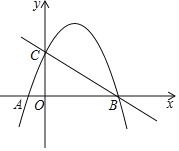
【题目】抛物线
经过点A（-1,0）、B（4,0），与y轴交于点C（0,4）.
(1)求抛物线的表达式；
(2)点P为直线BC上方抛物线的一点，分别连接PB、PC，若直线BC恰好平分四边形COBP的面积，求P点坐标；
(3)在（2）的条件下，是否在该抛物线上存在一点Q,该抛物线对称轴上存在一点N，使得以A、P、Q、N为顶点的四边形为平行四边形？若存在，求出Q点坐标，若不存在，请说明理由.
【答案】（1）
；（2）点P坐标为（2,6）；（3）Q点坐标为（
，-
)或（
，
）.
【解析】（1）把A、B、C三点坐标代入抛物线y=ax2+bx+c中，求出a、b、c的值即可；
（2）设P点坐标为（x，-x2+3x+4），根据四边形COBP的面积=S△COP+ S△BOP以及四边形COBP的面积=2S△COB求解即可；
(3)分AQ和AN分别为对角线时进行讨论可得解.
（1）把A（-1，0）、B（4，0）、C（0，4）三点坐标代入抛物线y=ax2+bx+c得，
,
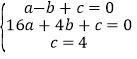解得：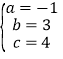
故抛物线的表达式为：y=-x2+3x+4；
（2）设P点坐标为（x，-x2+3x+4），如图，
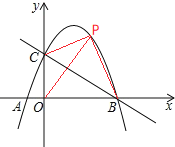
∴四边形COBP的面积=S△COP+ S△BOP=
=-2x2+8x+8
∵直线BC平分四边形COBP的面积
∴四边形COBP的面积=2S△COB
即：-2x2+8x+8=
解得x=2
将x=2代入抛物线表达式得y=6
故点P坐标为（2,6）
(3)存在
①当AQ为平行四边形的对角线时，Q点横坐标为，
故Q（
）
②当AN为平行四边形的对角线时，Q点横坐标为
，
故Q（
）
综上所述，Q点坐标为（)或（）
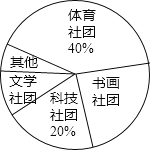
【题目】某校计划成立学生社团，要求每一位学生都选择一个社团，为了了解学生对不同社团的喜爱情况，学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查，规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项，并将统计结果绘制了如下两个不完整的统计图表．
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题：
（1）a= ，b= ；
（2）在扇形统计图中，“书画社团”所对应的扇形圆心角度数为 ；
（3）若该校共有3000名学生，试估计该校学生中选择“文学社团”的人数．
