题目内容
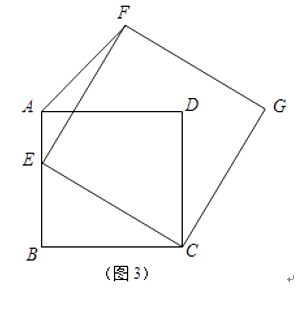
【题目】如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A,B),过B,C,E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.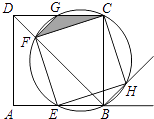
(1)求证:四边形EFCH是正方形;
(2)设BE=x,△CFG的面积为y,求y与x的函数关系式,并求y的最大值.
【答案】
(1)证明:∵B、H、C、F、E在同一圆上,且∠EBC=90°
∴∠EFC=90°,∠EHC=90°,
又∵∠FBC=∠HBC=45°,
∴CF=CH,
∵∠HBF+∠HCF=180°,
∴∠HCF=90°,
∴四边形EFCH是正方形
(2)解:∵∠BFG+∠BCG=180°,
∴∠BFG=90°,
由(1)知∠EFC=90°,
∴∠CFG+∠BFC=∠BFE+∠BFC,
∴∠CFG=∠BFE,
∴CG=BE=x,
∴DG=DC﹣CG=1﹣x,
易知△DFG是等腰直角三角形,
∴△CFG中CG边上的高为 ![]() DG=
DG= ![]() (1﹣x),
(1﹣x),
∴y= ![]() x
x ![]() (1﹣x)=﹣
(1﹣x)=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() ,
,
∴当x= ![]() 时,y有最大值
时,y有最大值 ![]()
【解析】(1)利用圆内接四边形性质,圆周角定理,须证三个角是直角,再证一组邻边相等可得出结论;(2)利用圆内接四边形的性质可得CG=BE=x,△DFG是等腰直角三角形,利用“直角三角形斜边中线等于斜边一半”可得△CFG中CG边上的高为 ![]() DG,列出二次函数关系式,配成顶点式求出最大值.
DG,列出二次函数关系式,配成顶点式求出最大值.

练习册系列答案
相关题目