Question

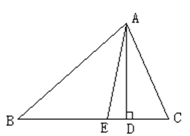
【题目】如图，A、B两个码头分别在一条河的两岸AC、BD上，河岸AC、BD均为东西走向，一艘客轮以每小时30千米的速度由A码头出发沿北偏东50°的方向航行至B码头，用时1.2小时，求该河的宽度（结果精确到1千米）
【参考数据：sin50°=0.77，cos50°=0.64，tan50°=1.20】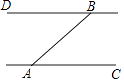

Answer 1

【答案】解：过点A作AH⊥BD于点H，

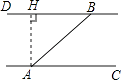
由题意可得：∠HAB=50°，AB=30×1.2=36（m），

在Rt△ABH中，∠AHB=90°，

∵cos∠HAB= ，

∴AH=ABcos∠HAB=36cos50°=36×0.64=23.04≈23（m），

答：该河的宽度约为23m．

【解析】通过作垂线构造直角三角形，把已知角放到直角三角形中，利用50度角的余弦联系直角边和斜边的关系，求出河宽.