题目内容
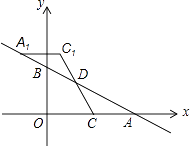
【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
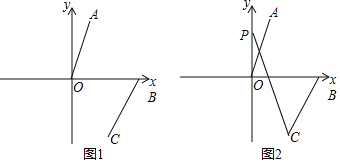
(1)直接写出A、B两点坐标为:A ,B ;
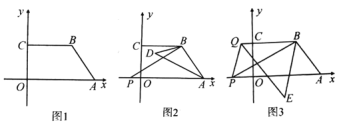
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
【答案】(1)A(1,3); B(3,0);(2)S四边形AOCB=9;(3)∠BCP﹣∠CPO=90°﹣a.
【解析】
(1)根据算术平方根、二次根式和偶次幂解答即可;
(2)根据平移的性质和三角形的面积解答即可;
(3)过点P作PD∥OA,可证得PD∥OA∥BC,由平行线的性质进行解答即可.
(1)∵a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
∴m=﹣3,n=2,a=3,b=3,
∴A(1,3),B(3,0);
故答案为:A(1,3); B(3,0);
(2)如图1所示:
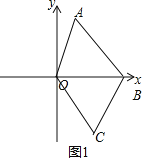
由题意知:C(2,﹣3),
∵B(3,0),
∴OB=3,
∴S四边形AOCB=S△AOB+S△BOC=![]() ,
,
故答案为:9;
(3)过点P作PD∥OA,如图2所示:

∵OA∥BC,
∴PD∥OA∥BC
∴∠BCP=∠DPC,∠DPO=∠AOP.
∵∠AOB=a,
∴∠AOP=90°﹣∠AOB=90°﹣a.
∴∠DPO=90°﹣a.
∵∠DPC=∠DPO+∠CPO,
∴∠BCP=∠CPO+90°﹣a,
即∠BCP﹣∠CPO=90°﹣a,
故答案为:∠BCP﹣∠CPO=90°﹣a.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目