题目内容
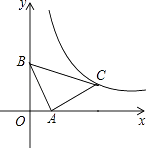
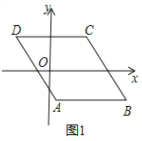
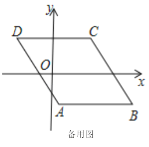
【题目】如图1，已知ABCD，AB∥x轴，AB＝6，点A的坐标为（1，﹣4），点D的坐标为（﹣3，4），点B在第四象限，点P是ABCD边上的一个动点．
（1）若点P在边BC上，PD＝CD，求点P的坐标．
（2）若点P在边AB，AD上，点P关于坐标轴对称的点Q落在直线y＝x﹣1上，求点P的坐标．
【答案】（1）（3，4）（2）点P的坐标为（﹣3，4）或（﹣1，0）或（5，﹣4）或（3，﹣4）
【解析】
（1）由题意点P与点C重合，可得点P坐标为（3，4）；（2）分两种情形①当点P在边AD上时，②当点P在边AB上时，假设出P点坐标，在每种情况中再分情况讨论，分别求出点P关于x轴和y轴的对称点，代入直线解析式列出方程即可解决问题；
（1）∵点A的坐标为（1，﹣4），点D的坐标为（﹣3，4），点B在第四象限，
∴∠DCB>90°，即PD为最长边，
∵PD=CD，
∴点P与点C重合，
∵CD＝AB=6，D（-3，4），
∴点P坐标为（3，4）．
（2）①当点P在边AD上时，
∵A（1，-4），D（-3，4），
∴直线AD的解析式为y＝﹣2x﹣2，
设P（a，﹣2a﹣2），且﹣3≤a≤1，
∴点P关于x轴的对称点为Q1（a，2a+2），
∵Q1在直线y＝x﹣1上，
∴2a+2＝a﹣1，
解得a＝﹣3，
此时P（﹣3，4）．
∵点P关于y轴的对称点为Q3（﹣a，﹣2a﹣2），且Q3在直线y＝x﹣1上时，
∴﹣2a﹣2＝﹣a﹣1，
解得a＝﹣1，
此时P（﹣1，0）
②当点P在边AB上时，设P（a，﹣4）且1≤a≤7，
∵P关于x轴的对称点为Q2（a，4），且Q2在直线y＝x﹣1上，
∴4＝a﹣1，
解得a＝5，
此时P（5，﹣4），
∵点P关于y轴的对称点为Q4（﹣a，﹣4），且Q4在直线y＝x﹣1上，
∴﹣4＝﹣a﹣1，
解得a＝3，
此时P（3，﹣4），
综上所述，点P的坐标为（﹣3，4）或（﹣1，0）或（5，﹣4）或（3，﹣4）．
