Question

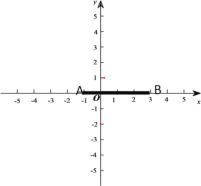
【题目】如图，在平面直角坐标系中，已知点A（2，0），点B（1，3）．

（1）画出将△OAB绕原点顺时针旋转90°后所得的△OA1B1，并写出点A1，B1的坐标；

（2）画出△OAB关于原点O的中心对称图形△OA2B2，并写出点A2，B2的坐标．

Answer 1

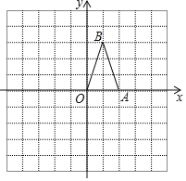
【答案】（1）画图见解析；A1（0，﹣2），B1（3，﹣1）；（2）画图见解析；A2（﹣2，0），B2（﹣1，﹣3）.

【解析】

（1）根据题意所述的旋转三要素找到各点的对应点，顺次连接可得出旋转后的图形，再由顺时针旋转90°后点的横坐标等于旋转前点的纵坐标，纵坐标等于旋转前点的横坐标的相反数，即可得出A′、B′的坐标；（2）根据题意找到各点的对应点，顺次连接可得出旋转后的图形，再由顺时针旋转后点的横坐标等于旋转前点的横坐标的相反数，纵坐标等于旋转前点的纵坐标的相反数，即可得A2、B2的坐标.

（1）如图，△OA1B1即为所求，A1（0，﹣2），B1（3，﹣1）；

（2）如图，△OA2B2即为所求，A2（﹣2，0），B2（﹣1，﹣3）；