题目内容
【题目】已知:点E为AB边上的一个动点.
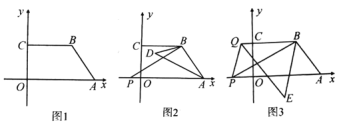
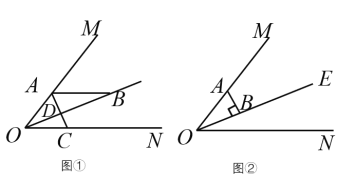
(1)如图1,若△ABC是等边三角形,以CE为边在BC的同侧作等边△DEC,连结AD.试比较∠DAC与∠B的大小,并说明理由;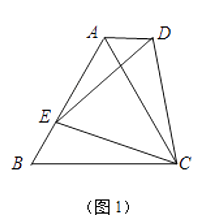
(2)如图2,若△ABC中,AB=AC,以CE为底边在BC的同侧作等腰△DEC,且△DEC∽△ABC,连结AD.试判断AD与BC的位置关系,并说明理由;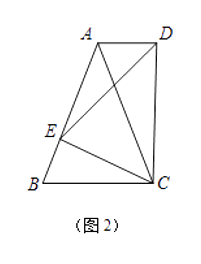
(3)如图3,若四边形ABCD是边长为2的正方形,以CE为边在BC的同侧作正方形ECGF.
①试说明点G一定在AD的延长线上;
②当点E在AB边上由点B运动至点A时,点F随之运动,求点F的运动路径长.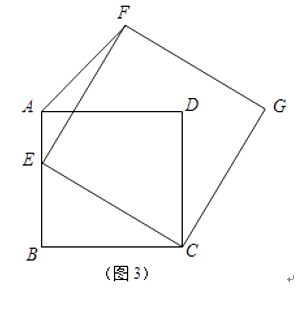
【答案】
(1)解:∠DAC=∠B
理由如下:
∵△ABC和△DEC都是等边三角形
∴∠DCE=∠ACB=60°
∴∠BCE=∠ACD
在△BEC和△ADC中,
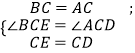
∴△BCE≌△ACD.
∴∠B=∠DAC
(2)解:AD∥BC
理由如下:
∵△ABC和△DEC都是等腰三角形,且△DEC∽△ABC
∴ ![]()
∵∠DCE=∠ACB,
∴∠DCA=∠ECB.
∴△DCA∽△ECB.
∴∠DAC=∠EBC=∠ACB.
∴AD∥BC
(3)解:①连结DG.
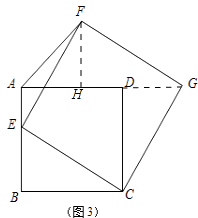
∵四边形ABCD和FECG都是正方形
∴BC=CD,CE=CG,∠BCD=∠ECG=90°.
∴∠BCE=∠DCG.
∴△BCE≌△DCG.
∴∠B=∠CDG=90°.
∵∠ADC=90°.
∴∠ADC+∠CDG=180°
∴点G一定在AD的延长线上.
②作FH⊥AG于点H.

∵∠BCE+ECD=90°,∠ECD+DCG=90°,
∴∠BCE=∠GCD.
∵∠GCD+∠CGD=90°,∠CGD+∠FGH=90°
∴∠FGH=∠GCD.
∴∠BCE=∠FGH=∠GCD.
在△FHG和△GDC和△EBC中,
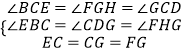 ,
,
∴△FHG≌△GDC≌△EBC,
∴FH=BE=DG,HG=BC,
∴AH=AG﹣GH=AD+DG﹣GH=BC+DG﹣BC=DG=FH,
∴△AFH是等腰直角三角形,
∴∠FAG=45°.
∴点F的运动路径长=AC= ![]() =2
=2 ![]()
【解析】(1)可观察后猜想两角相等,须证两角所在的三角形全等,即△BCE≌△ACD,得出∠B=∠DAC;(2)类比(1)的方法,观察图形,可猜想△DEC∽△ABC,进而证出△DCA∽△ECB,得出∠DAC=∠EBC=∠ACB,AD∥BC;(3)先研究起始位置A,由△FHG≌△GDC≌△EBC,可得△AFH是等腰直角三角形,F的运动方向为沿与AD夹角为45度方向移动,终点为F,点F的运动路径长=AC,利用勾股定理求出.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案