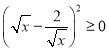题目内容
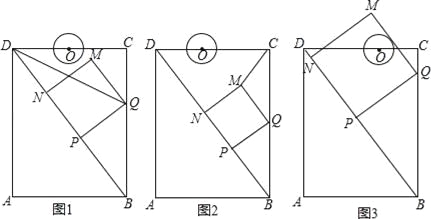
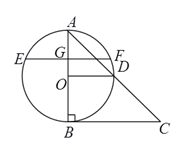
【题目】如图,在![]() 中,
中,![]() .以
.以![]() 为直径的⊙
为直径的⊙![]() 与
与![]() 相切于
相切于![]() ,交
,交![]() 于点
于点![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() ,过点作弦
,过点作弦![]() ,垂足为点
,垂足为点![]() .
.
(1)求证:①![]() ,②
,②![]() .
.
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(![]() )①证明见解析;②证明见解析;(
)①证明见解析;②证明见解析;(![]() )4
)4![]() .
.
【解析】(1) ①由切线的性质和垂径定理即可得证;(2)连接BD,由直径所对的圆周角为90°和等腰三角形的性质以及已知条件证明结论即可;(2)AB=2,则圆的直径为2,所以半径为1,即OB=OE=1,利用勾股定理求出CO的长,再通过证明△EOG∽△COB得到关于EG的比例式可求出EG的长,进而求出EF的长.
本题解析:
(![]() )①∵
)①∵![]() 为切线,切点为
为切线,切点为![]() ,
,![]() 为直径,∴
为直径,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
②连接![]() .
.
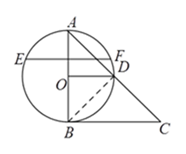
∵![]() 为直径,点
为直径,点![]() 在⊙
在⊙![]() 上,∴
上,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
(![]() )∵
)∵![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() ,
,![]() ,
,
∴(![]() )①∵
)①∵![]() 为切线,切点为
为切线,切点为![]() ,
,![]() 为直径,∴
为直径,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
②连接![]() .
.

∵![]() 为直径,点
为直径,点![]() 在⊙
在⊙![]() 上,∴
上,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
(![]() )∵
)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 即
即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目