题目内容
【题目】如图,A(0,1),M(3,2),N(4,4) , 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为 t 秒.(直线y = kx+b平移时k不变)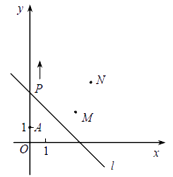
(1)当t=3时,求 l 的解析式;
(2)若点M,N位于l 的异侧,确定 t 的取值范围.
【答案】
(1)解:直线y=-x+b交y轴于点P(0,b),
由题意,得b>0,t≥0,b=1+t
当t=3时,b=4
∴y=-x+4
(2)解:当直线y=-x+b过M(3,2)时,2=-3+b解得b=5,
∴5=1+t∴t=4
当直线y=-x+b过N(4,4)时,4=-4+b解得 b=8
∴8=1+t∴t=7
∴4<t<7
【解析】当t=3时, 动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,得出点P的坐标,进而求出函数解析式。
(2)分别求出直线l 经过点M和经过点N时t的值,即可得到t的取值范围。
【考点精析】关于本题考查的确定一次函数的表达式,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能得出正确答案.

练习册系列答案
相关题目