题目内容
【题目】[探究函数
的图象与性质]
（1）函数
的自变量
的取值范围是 ；
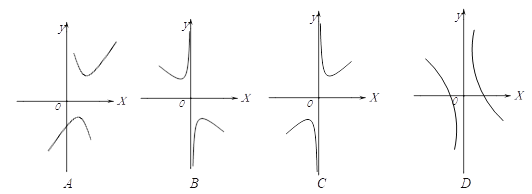
（2）下列四个函数图象中函数
的图象大致是 ；
（3）对于函数
，求当
时， 
的取值范围.
请将下列的求解过程补充完整.
解：∵
∴
∵
∴
.
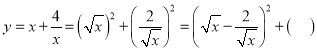
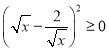
[拓展运用]
（4）若函数
，则
的取值范围 .
【答案】（1）
；（2）C；（3）4，4；（4）
【解析】试题分析：本题的⑴问抓住函数是由分式给定的，所以抓住是分母不为0,即可确定自变量的取值范围.本题的⑵问结合第⑴问中的
，即
或
进行分类讨论函数值
的大致取值范围，即可得到函数的大致图象.本题的第⑶问根据函数的配方逆向展开即推出“（ ）”应填写“常数”部分，再根据配方情况可以得到当当
时， 
的取值范围.本题的⑷问现将函数改写为
的形式，再按⑶的形式进行配方变形即可求
的取值范围.
试题解析：（1）由于函数
是分式给定的，所要满足分母不为0，所以
.
故填： 
.
（2）
即
或
；当
时， 
的值是正数，此时画出的图象只能在第一象限；当
时， 
的值是负数，此时画出的图象只能在第三象限；所以函数
的图象只在直角坐标系的一、三象限.故其大致图象应选C.
（3）∵
，
∴
.
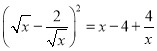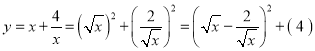故分别填： 
；
（4） ∵
（这里隐含有
首先是正数）
∴
∵
∴
.
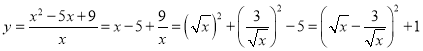
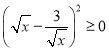
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
