题目内容
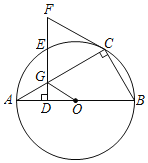
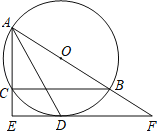
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC的延长线于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若AC=8,CE=4,求弧BD的长.(结果保留π)
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,由OA=OD知∠OAD=∠ODA,由AD平分∠EAF知∠DAE=∠DAO,据此可得∠DAE=∠ADO,继而知OD∥AE,根据AE⊥EF即可得证;
(2)作OG⊥AE,知AG=CG=![]() AC=4,证四边形ODEG是矩形,得出OA=OB=OD=CG+CE=4,再证△ADE∽△ABD得AD2=192,据此得出BD的长及∠BAD的度数,利用弧长公式可得答案.
AC=4,证四边形ODEG是矩形,得出OA=OB=OD=CG+CE=4,再证△ADE∽△ABD得AD2=192,据此得出BD的长及∠BAD的度数,利用弧长公式可得答案.
(1)证明:连接OD,如图1所示:

∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠EAF,
∴∠DAE=∠DAO,
∴∠DAE=∠ADO,
∴OD∥AE,
∵AE⊥EF,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)解:作OG⊥AE于点G,连接BD,如图2所示:

则AG=CG=![]() AC=4,∠OGE=∠E=∠ODE=90°,
AC=4,∠OGE=∠E=∠ODE=90°,
∴四边形ODEG是矩形,
∴OA=OB=OD=CG+CE=4+4=8,∠DOG=90°,
∴AB=2OA=16,
∵AC=8,CE=4,
∴AE=AC+CE=12,
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△ADE∽△ABD,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
在Rt△ABD中,![]() ,
,
在Rt△ABD中,∵AB=2BD,
∴∠BAD=30°,
∴∠BOD=60°,
则弧BD的长度为![]() =
=![]() .
.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案【题目】学校为了解九年级学生对“八礼四仪”的掌握情况,对该年级的500名同学进行问卷测试,并随机抽取了10名同学的问卷,统计成绩如下:
得分 | 10 | 9 | 8 | 7 | 6 |
人数 | 3 | 3 | 2 | 1 | 1 |
(1)计算这10名同学这次测试的平均得分;
(2)如果得分不少于9分的定义为“优秀”,估计这 500名学生对“八礼四仪”掌握情况优秀的人数;
(3)小明所在班级共有40人,他们全部参加了这次测试,平均分为7.8分.小明的测试成绩是8分,小明说,我的测试成绩在班级中等偏上,你同意他的观点吗?为什么?