Question

【题目】如图，矩形纸片ABCD，将△AMP和△BPQ分别沿PM和PQ折叠（AP＞AM），点A和点B都与点E重合；再将△CQD沿DQ折叠，点C落在线段EQ上点F处．

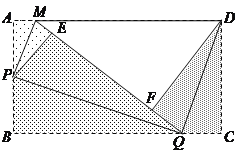
（1）判断△AMP，△BPQ，△CQD和△FDM中有哪几对相似三角形？（不需说明理由）

（2）如果AM＝1，sin∠DMF＝，求AB的长．

Answer 1

【答案】（1）△AMP∽△BPQ∽△CQD；（2）AB=6.

【解析】

根据题意得出三对相似三角形；设AP=x，有折叠关系可得：BP=AP=EP=x，AB=DC=2x，AM=1，根据△AMP∽△BPQ得：即，根据由△AMP∽△CQD得：即CQ=2，从而得出AD=BC=BQ+CQ=+2，MD=AD－AM=+2－1=+1，根据Rt△FDM中∠DMF的正弦值得出x的值，从而求出AB的值.

（1）有三对相似三角形，即△AMP∽△BPQ∽△CQD

（2）设AP=x，有折叠关系可得：BP=AP=EP=x AB=DC=2x AM=1

由△AMP∽△BPQ得：即

由△AMP∽△CQD得：即CQ=2

AD=BC=BQ+CQ=+2 MD=AD－AM=+2－1=+1

又∵在Rt△FDM中，sin∠DMF=DF=DC=2x

∴

解得：x=3或x=（不合题意，舍去）

∴AB=2x=6.