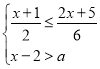Question

【题目】如图，已知抛物线y＝x2+bx+c与x轴相交于A（﹣1，0），B（m，0）两点，与y轴相交于点C（0，﹣3），抛物线的顶点为D．

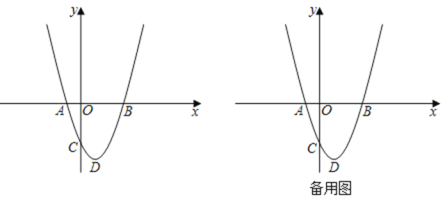
（1）求B、D两点的坐标；

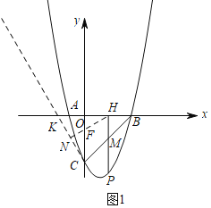
（2）若P是直线BC下方抛物线上任意一点，过点P作PH⊥x轴于点H，与BC交于点M，设F为y轴一动点，当线段PM长度最大时，求PH+HF+CF的最小值；

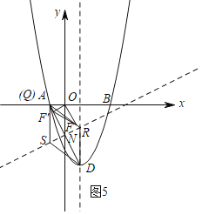
（3）在第（2）问中，当PH+HF+CF取得最小值时，将△OHF绕点O顺时针旋转60°后得到△OH′F′，过点F′作OF′的垂线与x轴交于点Q，点R为抛物线对称轴上的一点，在平面直角坐标系中是否存在点S，使得点D、Q、R、S为顶点的四边形为菱形，若存在，请直接写出点S的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）B（3，0），D（1，﹣4）；（2）；（3）存在，S的坐标为（3，0）或（﹣1，﹣2）或（﹣1，2）或（﹣1，﹣）

【解析】

（1）将A（﹣1，0）、C（0，﹣3）代入y＝x2+bx+c，待定系数法即可求得抛物线的解析式，再配方即可得到顶点D的坐标，根据y＝0，可得点B的坐标；

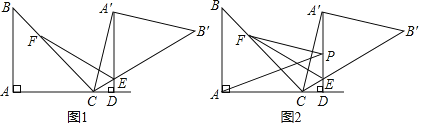
（2）根据BC的解析式和抛物线的解析式，设P（x，x2﹣2x﹣3），则M（x，x﹣3），表示PM的长，根据二次函数的最值可得：当x＝时，PM的最大值，此时P（，﹣），进而确定F的位置：在x轴的负半轴了取一点K，使∠OCK＝30°，过F作FN⊥CK于N，当N、F、H三点共线时，如图2，FH+FN最小，即PH+HF+CF的值最小，根据含30°角的直角三角形的性质，即可得结论；

（3）先根据旋转确定Q的位置，与点A重合，根据菱形的判定画图，分4种情况讨论：分别以DQ为边和对角线进行讨论，根据菱形的边长相等和平移的性质，可得点S的坐标．

（1）把A（﹣1，0），点C（0，﹣3）代入抛物线y＝x2+bx+c，得：

，解得：，

∴抛物线的解析式为：y＝x2﹣2x﹣3＝（x﹣1）2﹣4，

∴顶点D（1，﹣4），

当y＝0时，x2﹣2x﹣3＝0，解得：x＝3或﹣1，

∴B（3，0）；

（2）∵B（3，0），C（0，﹣3），

设直线BC的解析式为：y＝kx+b，

则 ，解得：，

∴直线BC的解析式为：y＝x﹣3，

设P（x，x2﹣2x﹣3），则M（x，x﹣3），

∴PM＝（x﹣3）﹣（x2﹣2x﹣3）＝﹣x2+3x＝﹣（x﹣）2+，

当x＝时，PM有最大值，此时P（，﹣），

在x轴的负半轴了取一点K，使∠OCK＝30°，过F作FN⊥CK于N，

∴FN＝CF，

当N、F、H三点共线时，如图1，FH+FN最小，即PH+HF+CF的值最小，

∵Rt△OCK中，∠OCK＝30°，OC＝3，

∴OK＝，

∵OH＝，

∴KH＝+，

∵Rt△KNH中，∠KHN＝30°，

∴KN＝KH＝，

∴NH＝KN＝，

∴PH+HF+CF的最小值=PH+NH＝＝；

（3）Rt△OFH中，∠OHF＝30°，OH＝，

∴OF＝OF'＝，

由旋转得：∠FOF'＝60°

∴∠QOF'＝30°，

∴在Rt△QF'O中，QF'＝OF'÷=÷＝，OQ=2QF'=2×=1，

∴Q与A重合，即Q（﹣1，0）

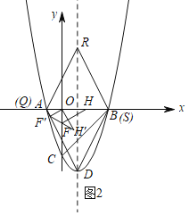
分4种情况：

①如图2，以QD为边时，由菱形和抛物线的对称性可得S（3，0）；

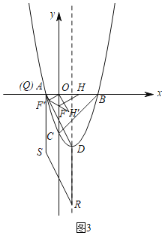
②如图3，以QD为边时，

由勾股定理得：AD＝，

∵四边形DQSR是菱形，

∴QS＝AD＝2，QS∥DR，

∴S（﹣1，﹣2）；

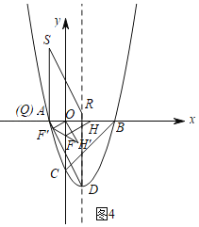
③如图4，同理可得：S（﹣1，2）；

④如图5，作AD的中垂线，交对称轴于R，可得菱形QSDR，

∵A（﹣1，0），D（1，﹣4），

∴AD的中点N的坐标为（0，﹣2），且AD＝2，

∴DN＝，

cos∠ADR＝，

∴DR＝，

∴QS= DR＝，

∴S（﹣1，﹣）；

综上，S的坐标为（3，0）或（﹣1，﹣2）或（﹣1，2）或（﹣1，﹣）．