Question

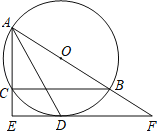
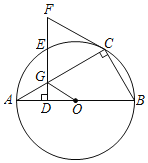
【题目】如图，Rt△ABC内接于⊙O，∠BCA＝90°，∠CBA＝60°，AB＝10，点D是AB边上（异于点A，B）的一动点，DE⊥AB交⊙O于点E，交AC于点G，交切线CF于点F．

（1）求证：FC＝CG；

（2）①当AE＝　 　时，四辺形BOEC为菱形；

②当AD＝　 　时，OG∥CF．

Answer 1

【答案】（1）见解析；（2）①5，②

【解析】

（1）连接OC，根据切线的性质得到∠OCF＝90°，证明△FCG为等边三角形，根据等边三角形的性质证明结论；

（2）①根据菱形的性质得到CE＝CB，得到△AOE为等边三角形，得到答案；

②根据平行线的性质得到∠GOC＝∠OCF＝90°，根据等边三角形的性质计算即可．

（1）证明：如图1，连接OC，

∵CF是⊙O的切线，

∴∠OCF＝90°，

∵∠BCA＝90°，∠CBA＝60°，

∴∠BAC＝30°，又DE⊥AB，

∴∠AGD＝60°，

∵OA＝OC，

∴∠OCA＝∠BAC＝30°，

∴∠FCG＝60°，又∠FGC＝∠AGD＝60°，

∴△FCG为等边三角形，

∴FC＝CG；

（2）解：①如图2，四边形BOEC为菱形时，CE＝CB，

∴

∴∠EAC＝∠BAC＝30°，又OE＝OA，

∴△AOE为等边三角形，

∴AE＝AO＝5，

故答案为：5；

②如图1，∵∠CBA＝60°，OC＝OB，

∴△BOC为等边三角形，

∴∠BOC＝60°，

∵OG∥CF，

∴∠GOC＝∠OCF＝90°，

∴∠AOG＝30°，

∴GA＝GO，又GD⊥AO，

∴AD＝AO＝，

故答案为：．