题目内容
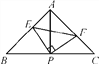
【题目】在△ABC中，AB=AC，点E，F分别在AB，AC上，AE=AF，BF与CE相交于点P．求证：PB=PC，并直接写出图中其他相等的线段．
【答案】证明见试题解析，PE=PF，BE=CF，BF=CE．
【解析】试题分析：可证明△ABF≌△ACE，则BF=CE，再证明△BEP≌△CFP，则PB=PC，从而可得出PE=PF，BE=CF．
试题解析：在△ABF和△ACE中，∵AB=AC，∠BAF=∠CAE，AF=AE，
∴△ABF≌△ACE（SAS），∴∠ABF=∠ACE，∴BF=CE，
∵AB=AC，AE=AF，∴BE=CF，
在△BEP和△CFP中，∵∠BPE=∠CPF，∠PBE=∠PCF，BE=CF，∴△BEP≌△CFP（AAS），∴PB=PC，
∵BF=CE，∴PE=PF，∴图中相等的线段为PE=PF，BE=CF，BF=CE．
练习册系列答案
相关题目
