题目内容
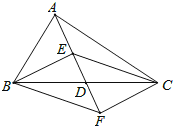
【题目】(8分)如图,△ABC的两条高AD、BE相交于点H,且AD=BD,试说明下列结论成立的理由。(1)∠DBH=∠DAC;(2)△BDH≌△ADC.

【答案】证明过程见解析
【解析】
试题分析:题目中有直角就可以得到角互余,再用互余的
性质就可以得到角相等,要证△BDH≌△ADC,只需根据
全等的判定找条件(1)中证了两个角,又已知一条边
即可证的全等.
试题解析:(1)∵ AD⊥BC,∴ ∠ADC=∠ADB=90°.
∵ BE⊥AC,∴ ∠BEA=∠BEC=90°.
∴ ∠DBH+∠C=90°,∠DAC+∠C=90°, ∴ ∠DBH=∠DAC.
(2)由(1)得∠DBH=∠DAC, ∠BDH=∠CDA=90° 又∵ AD=BD ,∴△BDH≌△ADC(ASA)

练习册系列答案
相关题目
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.