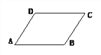
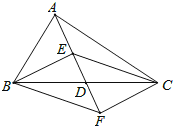
[题目]如图.在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE.∠FAB=∠EAD=90°.连结AC.EF．在图中找一个与△FAE全等的三角形.并加以证明．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE，∠FAB=∠EAD=90°，

连结AC、EF．在图中找一个与△FAE全等的三角形，并加以证明．

【答案】△FAE≌△ABC或△CDA，证明见解析.

【解析】

试题分析：∵∠BAD+∠EAF+∠FAB+∠EAD=360°，∠FAB=∠EAD=90°，∴∠BAD+∠EAF=180°∵四边形ABCD为平行四边形，∴∠BAD+∠ABC=180°，∴∠EAF=∠ABC（同角的补角相等）∵△ABF和△ADE都是等腰直角三角形，∴AF=AB,AE=AD又∵□ABCD中AD=BC（平行四边形的性质）∴AE=BC

∵在△FAE和△ABC中AF=AB，∠EAF=∠ABC，AE=BC，∴△FAE≌△ABC，又∵四边形ABCD为平行四边形△CDA≌△ABC∴△FAE≌△CDA

练习册系列答案

初中生必做的阅读理解与完形填空系列答案

（1）调查的总人数为　　；

（2）补全条形统计图；

（3）该单位共有2000人，为了积极践行“低碳生活，绿色出行”这种生活方式，调查后开私家车的人上下班全部改为骑自行车，则现在骑自行车的人数约为多少人？

【题目】某同学报名参加学校秋季运动会，有以下5个项目可供选择：径赛项目：100m、200m、1000m（分别用A1、A2、A3表示）；田赛项目：跳远，跳高（分别用T1、T2表示）．
（1）该同学从5个项目中任选一个，恰好是田赛项目的概率P为；
（2）该同学从5个项目中任选两个，求恰好是一个径赛项目和一个田赛项目的概率P1 ，利用列表法或树状图加以说明；
（3）该同学从5个项目中任选两个，则两个项目都是径赛项目的概率P2为．

【题目】下列哪组条件能够判别四边形ABCD是平行四边形？（　　）

A. AB∥CD，AD＝BC B. AB＝CD，AD＝BC

C. ∠A＝∠B，∠C＝∠D D. AB＝AD，CB＝CD

【题目】如图，在矩形ABCD中，E，F分别是边AB，CD上的点，AE=CF，连接EF，BF；EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC，FC=2，则AB的长为．

【题目】如图，在△ABC中，点D是BC的中点，点E，F分别在线段AD及其延长线上，且DE=DF．给出下列条件：

①BE⊥EC；②BF∥CE；③AB=AC；

从中选择一个条件使四边形BECF是菱形，你认为这个条件是（只填写序号）．

【题目】如图所示，在△ABC中，AD平分∠BAC，AD⊥BC，垂足为D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为E.

（1）求证：四边形ADCE是矩形；

（2）当△ABC满足什么条件时，四边形ADCE是正方形？给出证明.

【题目】（题文）正整数按图中的规律排列,请写出第18行,第20列的数字：_____．

【题目】在△ABC中，AB=AC，点E，F分别在AB，AC上，AE=AF，BF与CE相交于点P．求证：PB=PC，并直接写出图中其他相等的线段．

试题分类