题目内容
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AB=3,点M,N分别在线段AC,AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,若△DCM为直角三角形时,则AM的长为_____.
【答案】2或3![]() ﹣3
﹣3
【解析】
依据△DCM为直角三角形,需要分两种情况进行讨论:当∠CDM=90°时,△CDM是直角三角形;当∠CMD=90°时,△CDM是直角三角形,分别依据含30°角的直角三角形的性质以及等腰直角三角形的性质,即可得到AM的长.
解:分两种情况:
①如图,当∠CDM=90°时,△CDM是直角三角形,
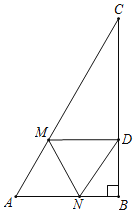
∵在Rt△ABC中,∠B=90°,∠A=60°,AB=3,
∴AC=2AB=6,∠C=30°,由折叠可得,∠MDN=∠A=60°,
∴∠BDN=30°,
∴BN=![]() DN=
DN=![]() AN,
AN,
∴BN=![]() AB=1,
AB=1,
∴AN=2BN=2,
∵∠DNB=60°,
∴∠ANM=∠DNM=60°,
∴∠AMN=60°,
∴AM=AN=2;
②如图,当∠CMD=90°时,△CDM是直角三角形,
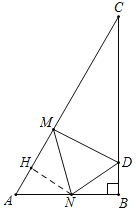
由题可得,∠CDM=60°,∠A=∠MDN=60°,
∴∠BDN=60°,∠BND=30°,
∴BD=![]() DN=
DN=![]() AN,BN=
AN,BN=![]() BD,
BD,
又∵AB=3,
∴AN=6(2﹣![]() ),BN=6
),BN=6![]() ﹣9,
﹣9,
过N作NH⊥AM于H,则∠ANH=30°,
∴AH=![]() AN=3(2﹣
AN=3(2﹣![]() ),HN=6
),HN=6![]() ﹣9,
﹣9,
由折叠可得,∠AMN=∠DMN=45°,
∴△MNH是等腰直角三角形,
∴HM=HN=6![]() ﹣9,
﹣9,
∴AM=AH+HM=3(2﹣![]() )+6
)+6![]() ﹣9=3
﹣9=3![]() ﹣3,
﹣3,
故答案为:2或3![]() ﹣3.
﹣3.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案【题目】小腾的爸爸计划将一笔资金用于不超过10天的短期投资,针对这笔资金,银行专属客户经理提供了三种投资方案,这三种方案的回报如下:
方案一:每一天回报30元;
方案二:第一天回报8元,以后每一天比前一天多回报8元;
方案三:第一天回报0.5元,以后每一天的回报是前一天的2倍.
下面是小腾帮助爸爸选择方案的探究过程,请补充完整:
(1)确定不同天数所得回报金额(不足一天按一天计算),如下表:
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
方案一 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
方案二 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
方案三 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
|
其中![]() ________;
________;
(2)计算累计回报金额,设投资天数为![]() (单位:天),所得累计回报金额是
(单位:天),所得累计回报金额是![]() (单位:元),于是得到三种方案的累计回报金额
(单位:元),于是得到三种方案的累计回报金额![]() ,
,![]() ,
,![]() 与投资天数
与投资天数![]() 的几组对应值:
的几组对应值:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
| 8 | 24 | 48 | 80 | 120 | 168 | 224 | 288 | 360 | 440 |
| 0.5 | 1.5 | 3.5 | 7.5 | 15.5 | 31.5 | 63.5 | 127.5 | 255.5 |
|
其中![]() ________;
________;
(3)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,
,![]() ,并画出
,并画出![]() ,
,![]() ,
,![]() 的图象;
的图象;
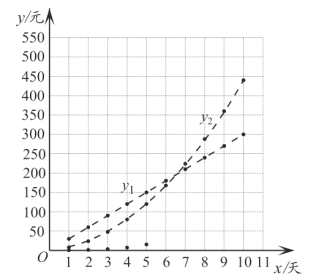
注:为了便于分析,用虚线连接离散的点.
(4)结合图象,小腾给出了依据不同的天数而选择对应方案的建议:
_________________________________________________________________________
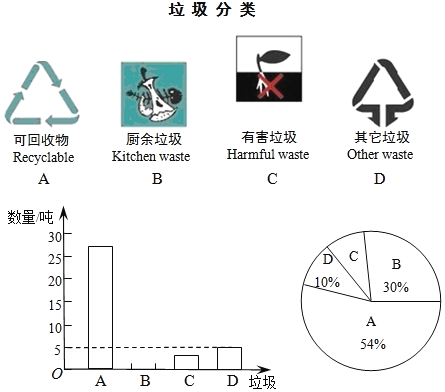
【题目】某校七年级有学生400人,为了解这个年级普及安全教育的情况,随机抽取了20名学生,进行安全教育考试,测试成绩(百分制)如下:
71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
(1)请补全七年级20名学生安全教育测试成绩频数分布直方图;
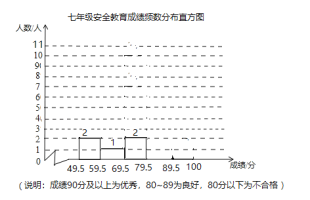
(2)样本数据的平均数、中位数、众数、优秀率如下表所示,请补充完整;
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 85.4 |
|
|
|
(3)估计七年级成绩优秀的学生人数约为_________人.
(4)学校有安全教育老师男女各2名,现从这4名老师中随机挑选2名参加“安全教育”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.