题目内容
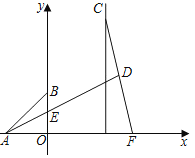
【题目】如图,AD是△ABC的中线,过点C作直线CF∥AD.
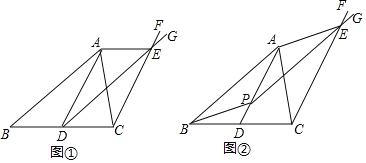
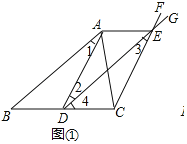
(问题)如图①,过点D作直线DG∥AB交直线CF于点E,连结AE,求证:AB=DE.
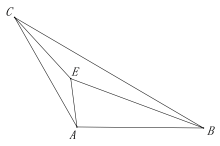
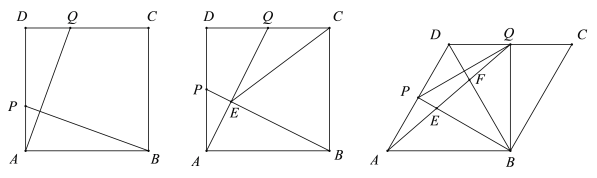
(探究)如图②,在线段AD上任取一点P,过点P作直线PG∥AB交直线CF于点E,连结AE、BP,探究四边形ABPE是哪类特殊四边形并加以证明.
(应用)在探究的条件下,设PE交AC于点M.若点P是AD的中点,且△APM的面积为1,直接写出四边形ABPE的面积.
【答案】【问题】:详见解析;【探究】:四边形ABPE是平行四边形,理由详见解析;【应用】:8.
【解析】
(1)先根据平行线的性质和等量代换得出∠1=∠3,再利用中线性质得到BD=DC,证明△ABD≌△EDC,从而证明AB=DE(2)方法一:过点D作DN∥PE交直线CF于点N,由平行线性质得出四边形PDNE是平行四边形,从而得到四边形ABPE是平行四边形.方法二: 延长BP交直线CF于点N,根据平行线的性质结合等量代换证明△ABP≌△EPN,
从而证明四边形ABPE是平行四边形(3)延长BP交CF于H,根据平行四边形的性质结合三角形的面积公式求解即可.
证明:如图①
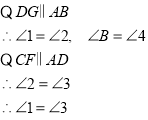
![]() 是
是![]() 的中线,
的中线,
![]()
![]()
![]()
(或证明四边形ABDE是平行四边形,从而得到![]() )
)
【探究】
四边形ABPE是平行四边形.
方法一:如图②,
证明:过点D作![]() 交直线
交直线![]() 于点
于点![]() ,
,

![]()
∴四边形![]() 是平行四边形,
是平行四边形,
![]()
∵由问题结论可得![]()
![]()
∴四边形![]() 是平行四边形.
是平行四边形.
方法二:如图③,
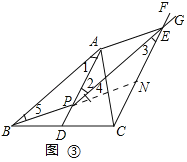
证明:延长BP交直线CF于点N,
![]()
![]()
![]()
![]()
![]()
∵![]() 是
是![]() 的中线,
的中线,![]()
![]()
![]()
![]()
∴四边形![]() 是平行四边形.
是平行四边形.
【应用】
如图④,延长BP交CF于H.
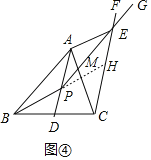
由上面可知,四边形![]() 是平行四边形,
是平行四边形,
![]()
![]()
∴四边形APHE是平行四边形,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目