Question

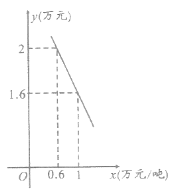
【题目】某蔬菜批发公司用实际行动支持抗击新冠肺炎疫情，为确保市民在疫情期间的蔬菜供应，以平均每吨万元的价格购进一批蔬菜，已知这批蔬菜通过网络在市场上的日销售量(吨)与销售价格(万元/吨)之间的函数关系如下图所示．

（1）求日销售量与销售价格之间的函数关系式； (不要求写的取值范围)

（2）如果要确保日销售量不小于吨，求最大毛利润．(假设：毛利润=销售额-购进成本)

Answer 1

【答案】（1）；（2）要确保日销售量不小于吨，最大毛利润为万元．

【解析】

（1）根据图象可知，销售量与销售价格之间的函数关系式为一次函数，且经过点，再利用待定系数法求解即可得；

（2）先根据“毛利润销售额购进成本”得出利润与x之间的函数关系式，再根据“日销售量不小于吨”求出x的取值范围，然后利用二次函数的性质求解即可得．

（1）由图象可知，销售量与销售价格之间的函数关系式为一次函数，且经过点

设销售量与销售价格之间的函数关系式为

将点代入得

解得

则与之间的函数关系式为；

（2）设销售毛利润为万元

则

配方得

由题意得，即

解得

由二次函数的性质可知，当时，随增大而增大；当时，随增大而减小

则当时，取最大值，最大值为万元

答：要确保日销售量不小于吨，最大毛利润为万元．